Capítulo 7 Modelos de panel

Francisco Urdinez³³

Lecturas sugeridas

Beck, N. (2008). Time‐Series Cross‐Section Methods. In J. M. Box-Steffensmeier, H. E. Brady, & D. Collier (Eds.), The Oxford Handbook of Political Methodology (pp. 475–493). Oxford: Oxford University Press.
Beck, N., & Katz, J. N. (2011). Modeling dynamics in time-series–cross-section political economy data. Annual Review of Political Science, 14, 331-352.
Croissant, Y., & Millo, G. (2018). Panel Data Econometrics with R. John Wiley and Sons.
Henningsen, A., & Henningsen, G. (2019). Analysis of Panel Data Using R. In M. Tsionas (Ed.), Panel Data Econometrics: Theory (pp. 345–396). London: Academic Press.

Los paquetes que necesitas instalar

tidyverse (Wickham 2019b), paqueteadp (Urdinez and Cruz 2020), unvotes (Robinson 2017), lubridate (Spinu, Grolemund, and Wickham 2020), ggcorrplot (Kassambara 2019), plm (Croissant, Millo, and Tappe 2020).

7.1 Introducción

En este capítulo, aprenderemos más sobre lo que hemos tocado en el capítulo de modelos lineales. Aprenderemos cómo trabajar con datos de panel, es decir, cómo añadir una dimensión temporal a nuestras regresiones lineales. Le mostraremos cómo diagnosticar si el tiempo tiene un efecto en nuestros resultados de MCO y de qué manera, y (a) estimar modelos con efectos fijos y efectos aleatorios, (b) ver cómo diagnosticar raíces unitarias, (c) cómo crear variables con desfases (llamados lags en inglés) o prospectivas (llamados leads en inglés), y (d) cómo calcular los errores estándar corregidos para panel. Recuerde que este es un capítulo introductorio, por lo que le recomendamos que consulte la bibliografía sugerida para responder a preguntas específicas.

Trabajaremos con un ejemplo práctico de relaciones internacionales: Históricamente, la política exterior de América Latina ha estado fuertemente influenciada por los Estados Unidos, probablemente más que cualquier otra región del mundo. Sin embargo, en los últimos treinta años, esta tendencia se ha debilitado, y la influencia es menos evidente ahora que durante la Guerra Fría. ¿Cuál es la razón de esta tendencia?

Esta pregunta fue abordada por Octavio Amorim Neto, un reconocido politólogo brasileño, en de Dutra a Lula: La formación y los determinantes de la política exterior brasileña* (De Dutra a Lula: a condução e os determinantes da política externa brasileira) (2012). Este libro tiene la ventaja de responder a esta pregunta con una metodología cuantitativa, algo inusual en un campo dominado por los trabajos historiográficos. Otros artículos pasaron luego a refinar más los argumentos del libro, como Neto and Malamud (2015) y Rodrigues, Urdinez, and de Oliveira (2019). Abramos la base de datos:

library(tidyverse)

library(paqueteadp)
data("eeuu_brasil")

Según Amorim Neto, a medida que Brasil se transformaba en una potencia regional, y su poder crecía, tenía un mayor margen para alejarse de los preceptos de los Estados Unidos. Una forma de abordar el concepto abstracto de “proximidad política” en las relaciones internacionales es a través de la convergencia de votos en la Asamblea General de las Naciones Unidas. Los países votan, digamos, 20 veces al año sobre diferentes temas. Así, sobre esos 20 votos, podemos calcular cuántas veces un país votó igual que otro (a favor, en contra o abstención) y expresar esta similitud como un porcentaje. La siguiente figura muestra el porcentaje de votos en común entre el Brasil y los Estados Unidos en la Asamblea de 1945:

ggplot(eeuu_brasil) + 
  geom_line(aes(x = anio, y = voto)) +
  labs(x = "Year", y = "Convergencia de votos")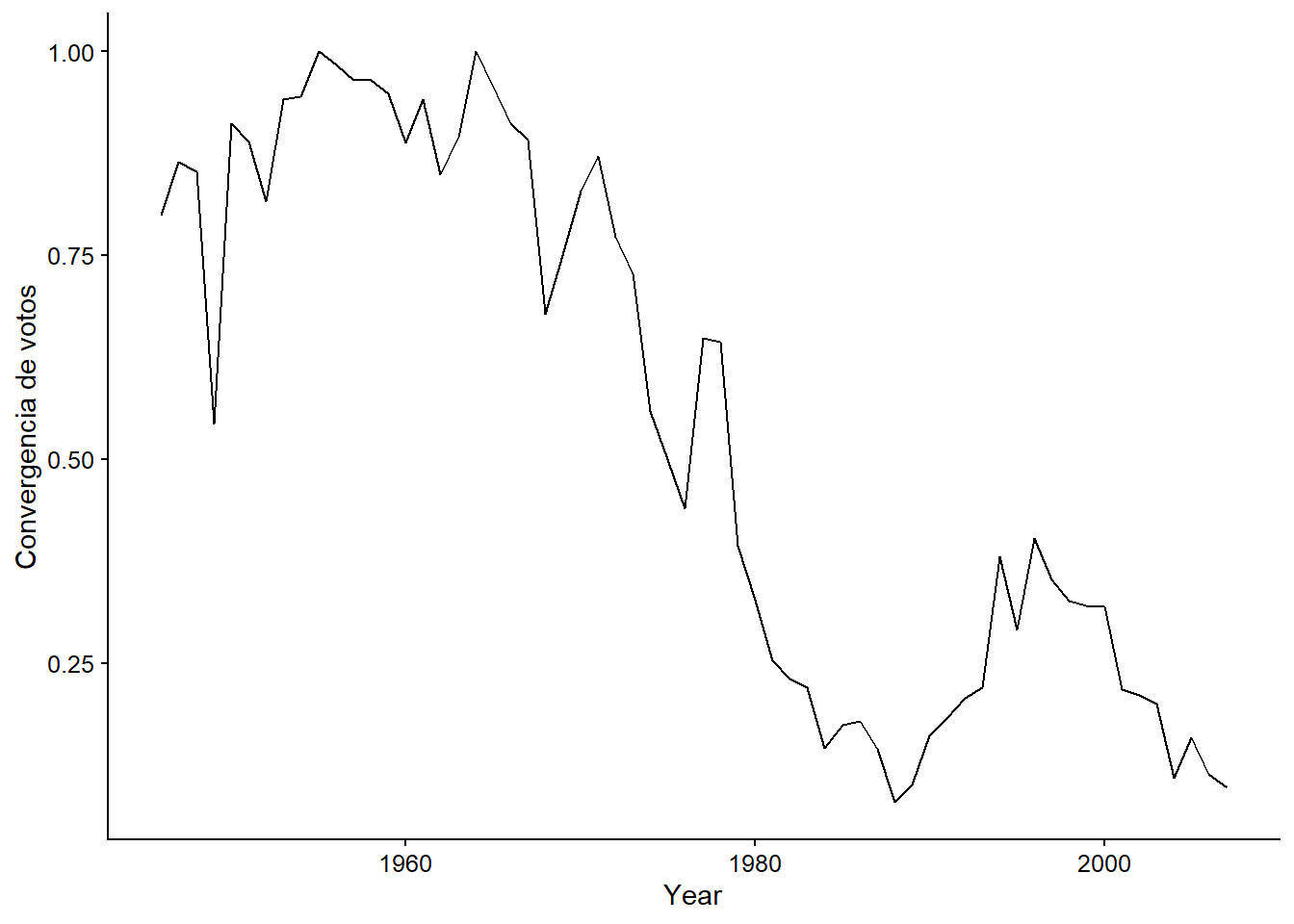

Figura 7.1: Convergencia de votos entre Brasil y los EE.UU.

Hay una herramienta sobresaliente llamada unvotes en R para todos aquellos que estudian la historia del voto de los países en la Asamblea de las Naciones Unidas, que nos será útil en este capítulo.³⁴. Usando unvotes podemos trazar la convergencia de los votos, y dividirlos por temas.

library(unvotes)
library(lubridate)

Además, haremos uso del paquete lubridate para el análisis con fechas.

El paquete unvotes proporciona tres bases de datos con los que podemos trabajar: un_roll_calls, un_roll_call_issues y eeuu_latam. Cada uno de estas bases de datos contiene una variable llamada rcid, el código de la votación, que puede ser usado como un identificador para unirlos con otras variables. Si recuerdas, en el capítulo de manejo avanzado te enseñamos cómo fusionar las bases de datos utilizando los códigos de país.

La base de datos de eeuu_latam proporciona información sobre el historial de votación de la Asamblea General de las Naciones Unidas. Contiene una fila para cada par de países votantes.
La base de datos un_roll_calls contiene información sobre cada votación nominal de la Asamblea General de las Naciones Unidas.
La base un_roll_call_issues contiene clasificaciones de temas de las votaciones nominales de la Asamblea General de las Naciones Unidas. Muchos votos no tienen ningún tema, y algunos tienen más de uno.

¿Cómo ha cambiado el registro de votación de los Estados Unidos a lo largo del tiempo en una variedad de temas en comparación con Brasil?

p_votos_eeuu_br <- un_votes %>%
  filter(country %in% c("United States of America", "Brazil")) %>%
  inner_join(un_roll_calls, by = "rcid") %>%
  inner_join(un_roll_call_issues, by = "rcid") %>%
  mutate(issue = if_else(issue == "Nuclear weapons",
                         "Nuclear weapons", issue)) %>%
  group_by(country, year = year(date), issue) %>%
  summarize(votes = n(),
            percent_yes = mean(vote == "yes")) %>%
  filter(votes > 5) 

ggplot(p_votos_eeuu_br,
       mapping = aes(x = year, y = percent_yes, color = country)) +
  geom_point() +
  geom_smooth(method = "loess", se = F) +
  facet_wrap(~ issue, ncol = 2) +
  scale_color_grey() +
  labs(x = "Year", y = "% Yes", color = "Country")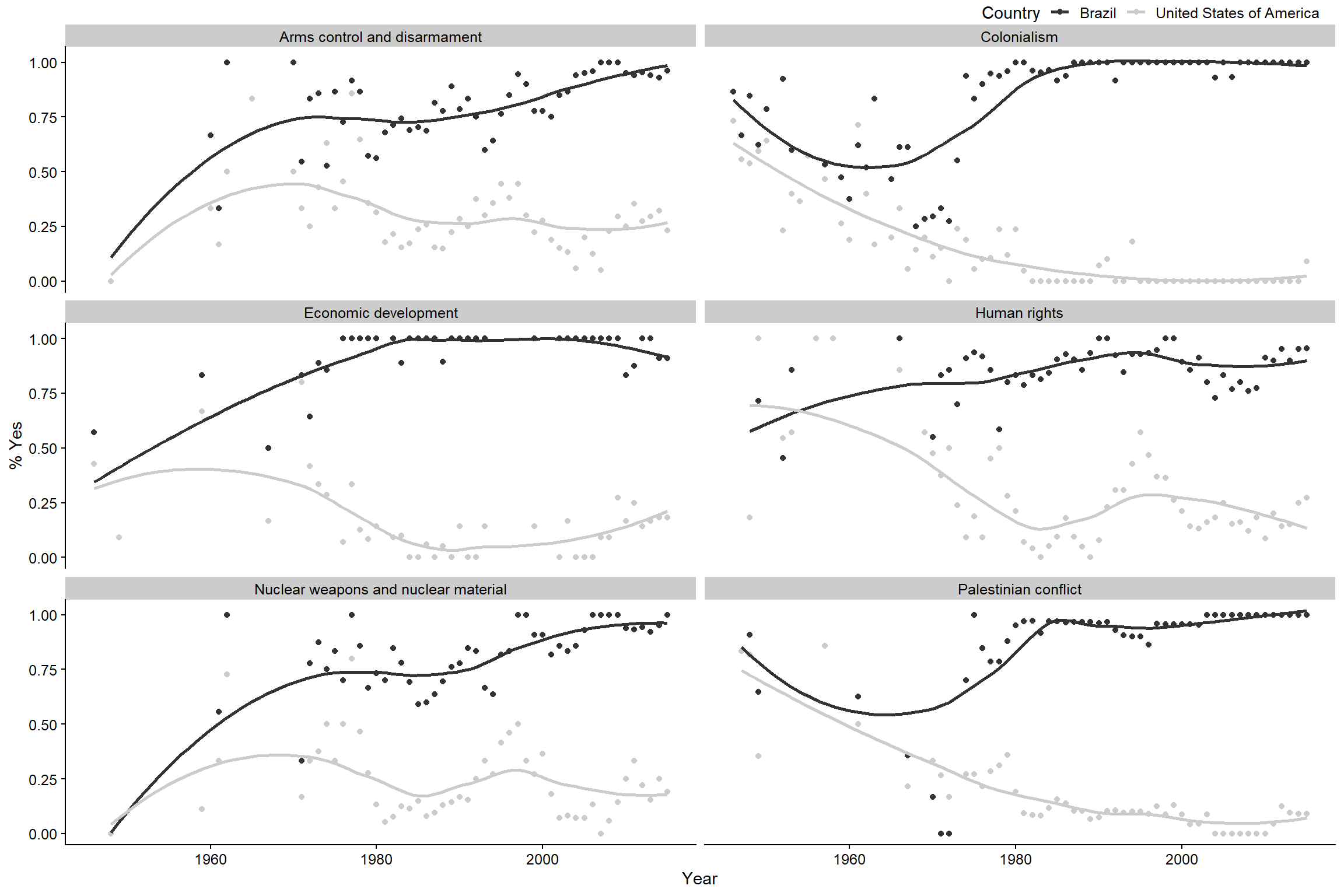

Figura 3.4: Porcentaje de votos positivos en la Asamblea General de la ONU (1946 a 2015)

Consideremos la hipótesis de Amorim Neto (2012). Su argumento es que este distanciamiento fue causado por un aumento del poder de Brasil, que le dio mayor autonomía. La discusión sobre cómo medir el poder en las relaciones internacionales es todo un tema en sí mismo. Una de las variables más populares para medirlo fue creada por Singer, Bremer, and Stuckey (1972)), conocida como el Índice CINC. Se trata de un índice relativo: para cada año, el índice mide la proporción de poder que cada país tiene del total del poder mundial. ¿Cómo ha cambiado Brasil desde 1945?

ggplot(eeuu_brasil) + 
  geom_line(aes(x = anio, y = poder_pais)) +
  labs(x = "Año", y = "Indice CINC")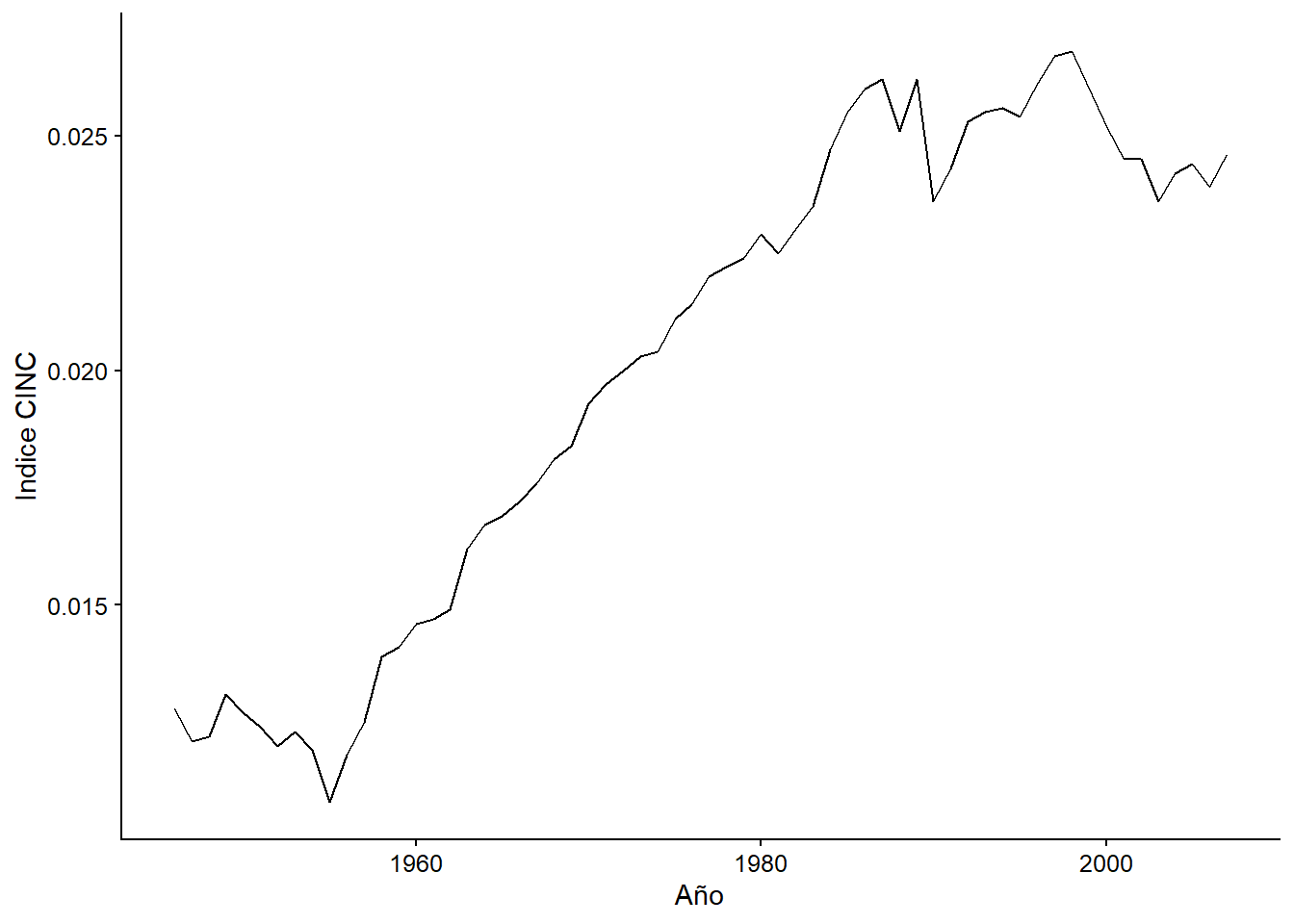

Figura 3.5: El poder internacional de Brasil

¡Muy bien! A priori, la hipótesis de Amorim Neto parece tener apoyo empírico: A medida que Brasil se volvió más poderoso, tuvo más margen para desarrollar una política exterior autónoma de los Estados Unidos. Si observamos la correlación entre ambas variables, observamos que ésta es alta y negativa (-0,89): los valores más altos de convergencia de votos están correlacionados con los valores más bajos de poder. Usaremos el paquete ggpubr para “Gráficas listas para publicar”:

library(ggpubr)

ggscatter(eeuu_brasil, x = "poder_pais", y = "voto",
          add = "reg.line",  add.params = list(color = "black", 
                                               fill = "lightgray"), 
          conf.int = TRUE) + 
  stat_cor(method = "pearson", label.x = 0.015)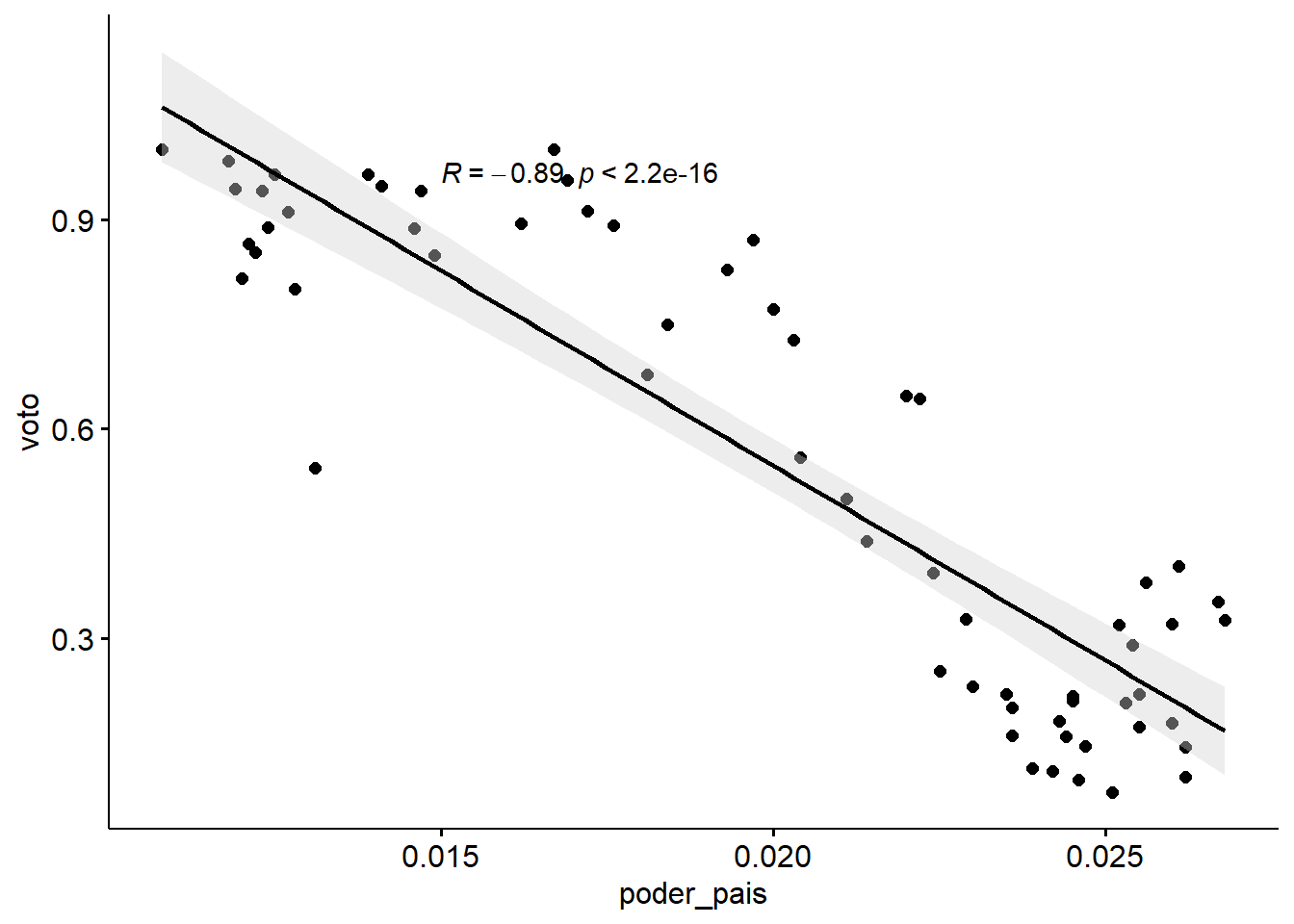

Figura 3.6: Correlación entre la convergencia de los votos de la ONU y la participación en el poder internacional

En conclusión, este es el argumento central del libro de Amorim Neto. A pesar de la gran influencia que este análisis tuvo sobre los estudios posteriores, hay algunas cuestiones que invalidan parcialmente la conclusión, que será útil ejemplificar en este capítulo.

7.2 Describiendo la base de datos en panel

En ciencias políticas, es común encontrar la distinción entre datos de panel y series temporales transversales (TSCS, en inglés). Beck (2008) explica que un panel se refiere a un conjunto de datos con una N mucho más grande que su T, por ejemplo, una encuesta de 10.000 personas durante tres años consecutivos. Por otro lado, una base de datos en formato TSCS a menudo contiene una T más grande que N, y sus unidades son fijas, es decir, se repiten en el tiempo. La distinción está muy bien desarrollada en un texto de Beck en Annual Review of Political Science:

“Los datos de panel son datos de secciones transversales repetidas, pero las unidades se muestrean (normalmente son encuestados obtenidos en algún esquema de muestreo aleatorio), y normalmente se observan sólo unas pocas veces. Las unidades de TSCS son fijas; no hay ningún esquema de muestreo para las unidades, y cualquier experimento de”remuestreo" debe mantener las unidades fijas y sólo remuestrear las unidades completas (Freedman & Peters 1984). En los datos en panel, las personas observadas no son de interés; todas las inferencias de interés se refieren a la población subyacente que fue objeto del muestreo, en lugar de estar condicionadas por la muestra observada. Los datos de la TSCS son exactamente lo contrario; todas las inferencias de interés son condicionales a las unidades observadas". (2001, 273).

A efectos prácticos, la notación de ambos es la misma y los conceptos tienden a utilizarse indistintamente: \[ y_i,_t = x_i,_t\beta + \epsilon_i,_t \] Donde \[ x_i,_t \] es un vector de variables exógenas y las observaciones son indexadas por ambas unidades (i) y tiempo (t).

Para revisar las rutinas más comunes de los modelos de panel, usaremos una base de datos similar a la de Amorim Neto, pero con once países sudamericanos. Ahora tenemos una base en formato TSCS: una muestra de once países entre 1970 y 2007, 38 años. Si domina el contenido introductorio de este capítulo, el siguiente paso será trabajar a través del libro de Croissant and Millo (2018), que también son los creadores del paquete más utilizado para el panel en R, plm.

data("eeuu_latam")

eeuu_latam %>% 
  count(pais)
## # A tibble: 10 x 2
##   pais          n
##   <chr>     <int>
## 1 Argentina    38
## 2 Bolivia      38
## 3 Brazil       38
## # ... with 7 more rows

Observemos la generalizabilidad de la hipótesis. El libro sólo analiza un caso, pero queremos saber si un panel de once países puede ayudarnos a fortalecer esos hallazgos y ganar validez externa. Si observamos el comportamiento de voto de estos once países latinoamericanos en las Naciones Unidas, notaremos un patrón similar entre ellos. Parece que la convergencia de votos con EE.UU. cayó entre 1945 y 1990, luego subió durante los 90, y luego volvió a caer a principios de los 2000. Siempre se recomienda hacer este paso antes de pasar a las regresiones. Hay dos formas de trazar las variables independientes y dependientes a lo largo del tiempo usando “ggplot2,” como ya has aprendido.

7.2.1 Opción A. Gráfico de líneas

ggplot(eeuu_latam, aes(x = anio, y = voto, 
                     color = pais, linetype = pais, group = pais)) + 
  geom_line() +
  labs(x = "Year", y = "% Yes", color = "", linetype = "")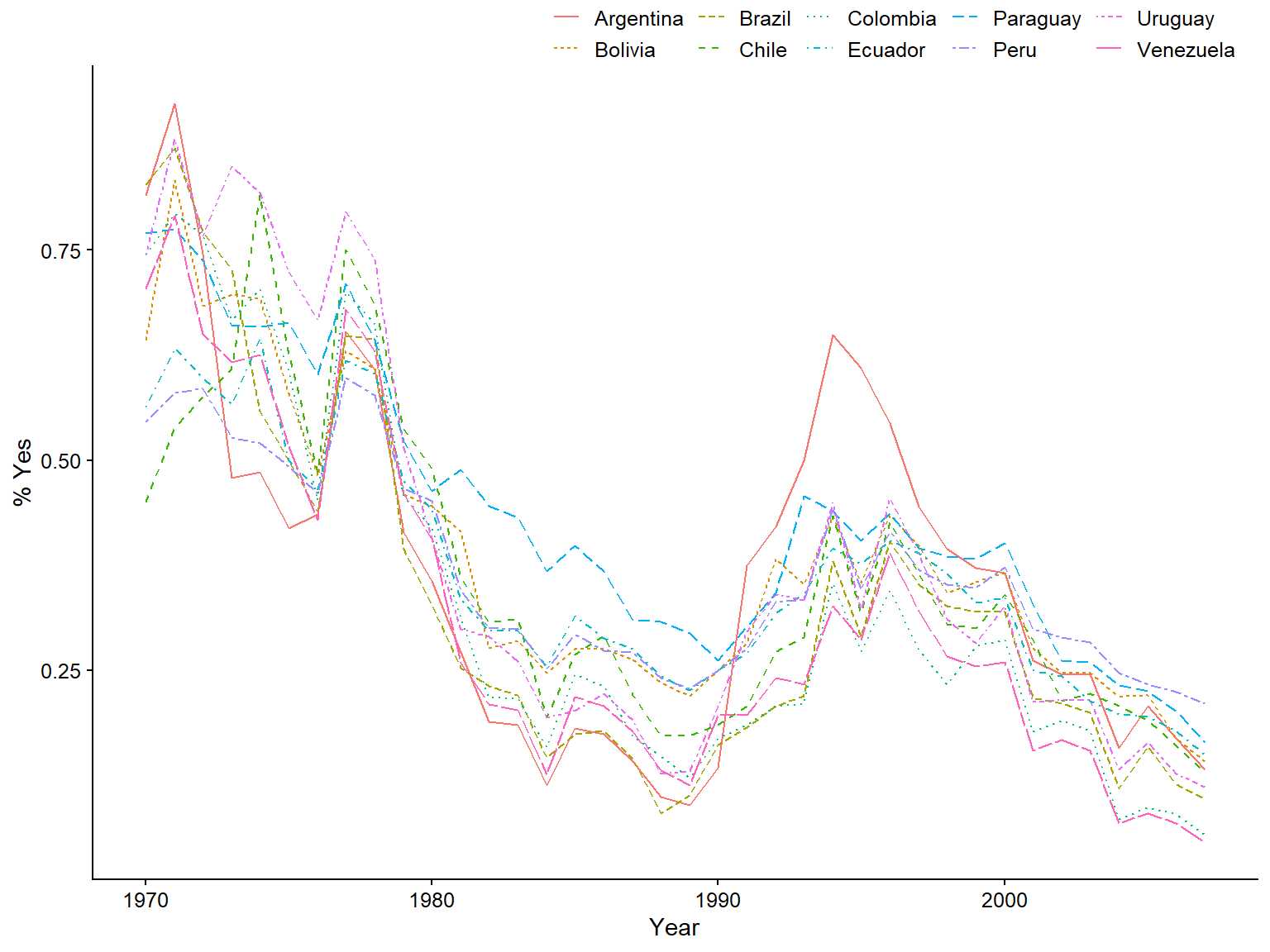

Figura 3.9: Tendencias de línea para la evolución de la convergencia de los votos de la AGNU con los de EE.UU. por país

7.2.2 Option B. Gráfico de cajas

ggplot(eeuu_latam, aes(x = factor(anio), y = voto)) +
  geom_boxplot() +
  scale_x_discrete(breaks = seq(1970, 2007, by = 5)) +
  labs(x = "Year", y = "% Convergencia con EEUU")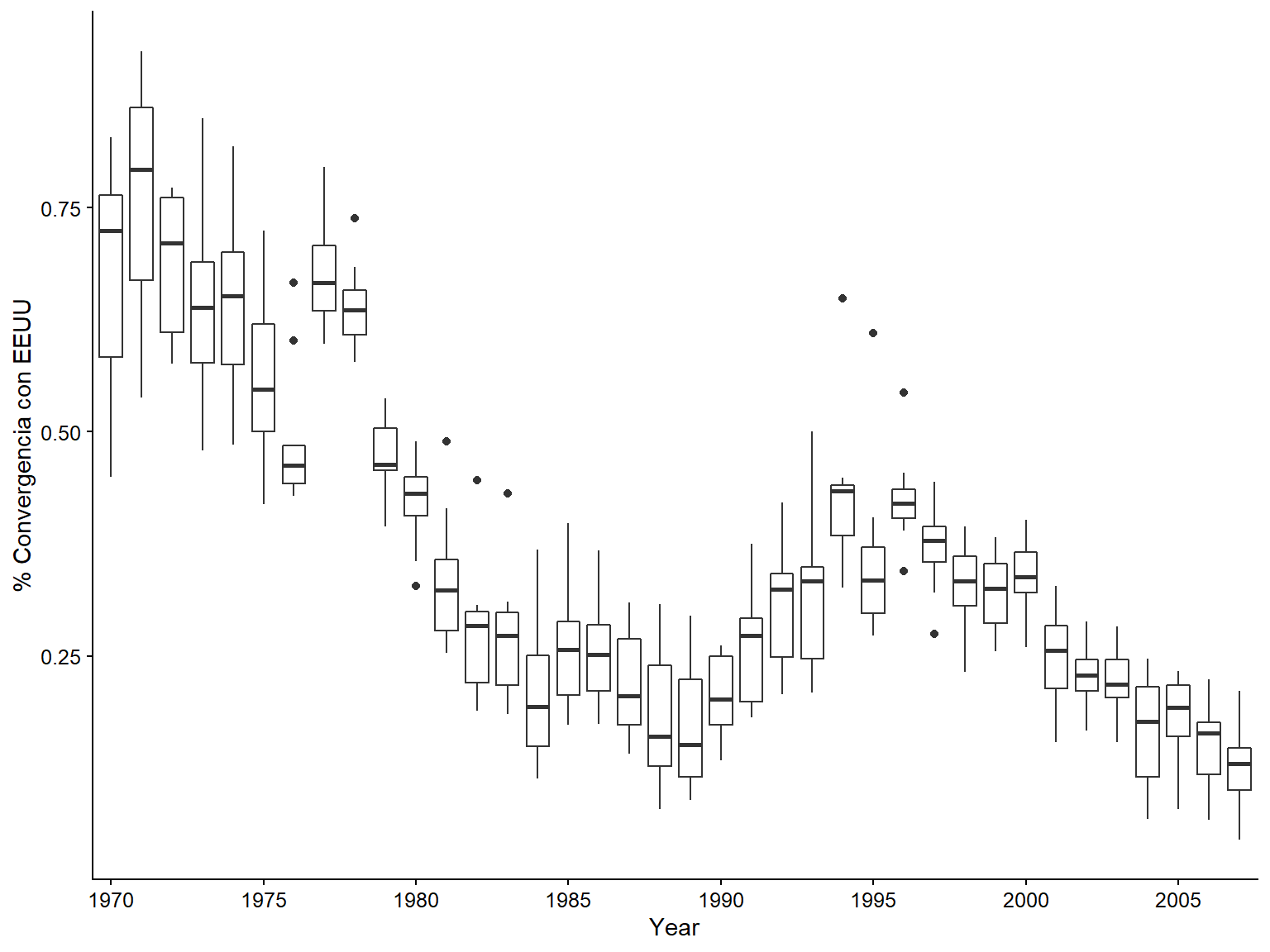

Figura 3.10: Gráficos de recuadro para la evolución de la convergencia de los votos de la AGNU con los de EE.UU. por país

Además, como observamos en el caso de Brasil, podemos ver la proximidad de los votos entre los 11 países y los Estados Unidos separando los votos por tema usando unvotes.

p_votos_paises <- un_votes %>%
  filter(country %in% c("United States of America", "Brazil", "Bolivia",
                     "Argentina", "Chile", "Peru", "Ecuador", "Colombia",
                     "Venezuela", "Paraguay", "Uruguay")) %>%
  inner_join(un_roll_calls, by = "rcid") %>%
  inner_join(un_roll_call_issues, by = "rcid") %>%
  mutate(issue = if_else(issue == "Nuclear weapons", 
                         "Nuclear weapons", issue)) %>%
  group_by(country, year = year(date), issue) %>%
  summarize(votes = n(),
            percent_yes = mean(vote == "yes")) %>%
  filter(votes > 5)

ggplot(p_votos_paises,
       mapping = aes(x = year, y = percent_yes, 
                     linetype = country, color = country)) +
  geom_smooth(method = "loess", se = F) +
  facet_wrap(~issue, ncol = 2) +
  labs(x = "Year", y = "% Convergencia con EEUU", color = "", linetype = "")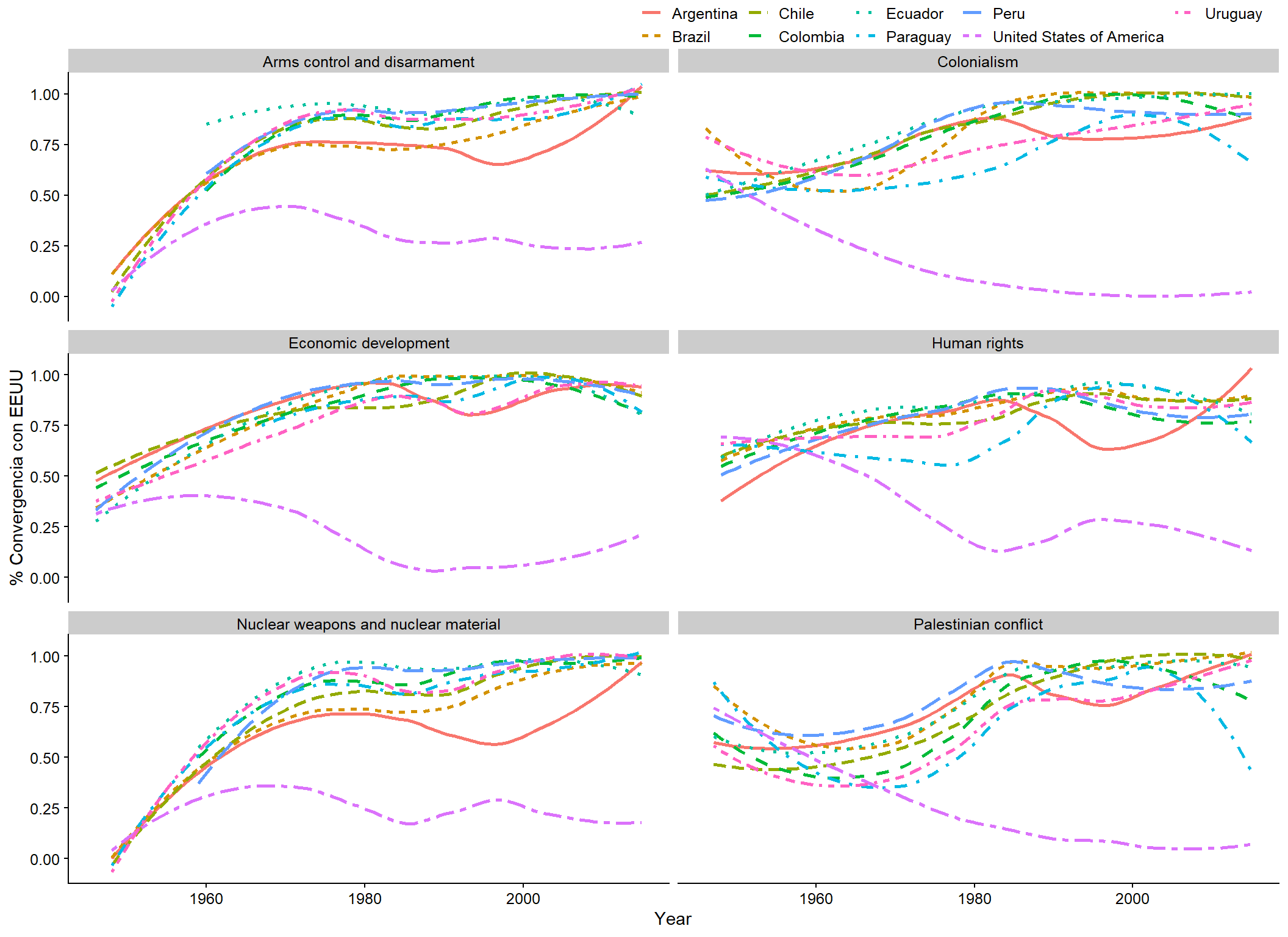

Figura 3.11: Porcentaje de votos positivos en la Asamblea General de la ONU (1946 a 2015)

Una vez que haya observado el comportamiento de su variable dependiente, probablemente querrá replicar el mismo ejercicio para su variable independiente. En nuestro caso, el poder del país. Al observar el comportamiento de la variable independiente de nuestro ejemplo (la potencia del país) notaremos que, mientras que Colombia está en línea con lo que observamos para Brasil (crecimiento de poder a lo largo de los años), otros países se han debilitado desde 1970 (por ejemplo, Argentina), y la mayoría de ellos se han mantenido prácticamente estables (por ejemplo, Chile, Uruguay y Perú). Esta heterogeneidad de comportamientos desafía los hallazgos de Amorim Neto para Brasil.

eeuu_latam %>% 
  filter(pais != "Brazil") %>% 
  ggplot(aes(x = anio, y = poder_pais)) + 
  geom_line() +
  facet_wrap(~pais, nrow = 3)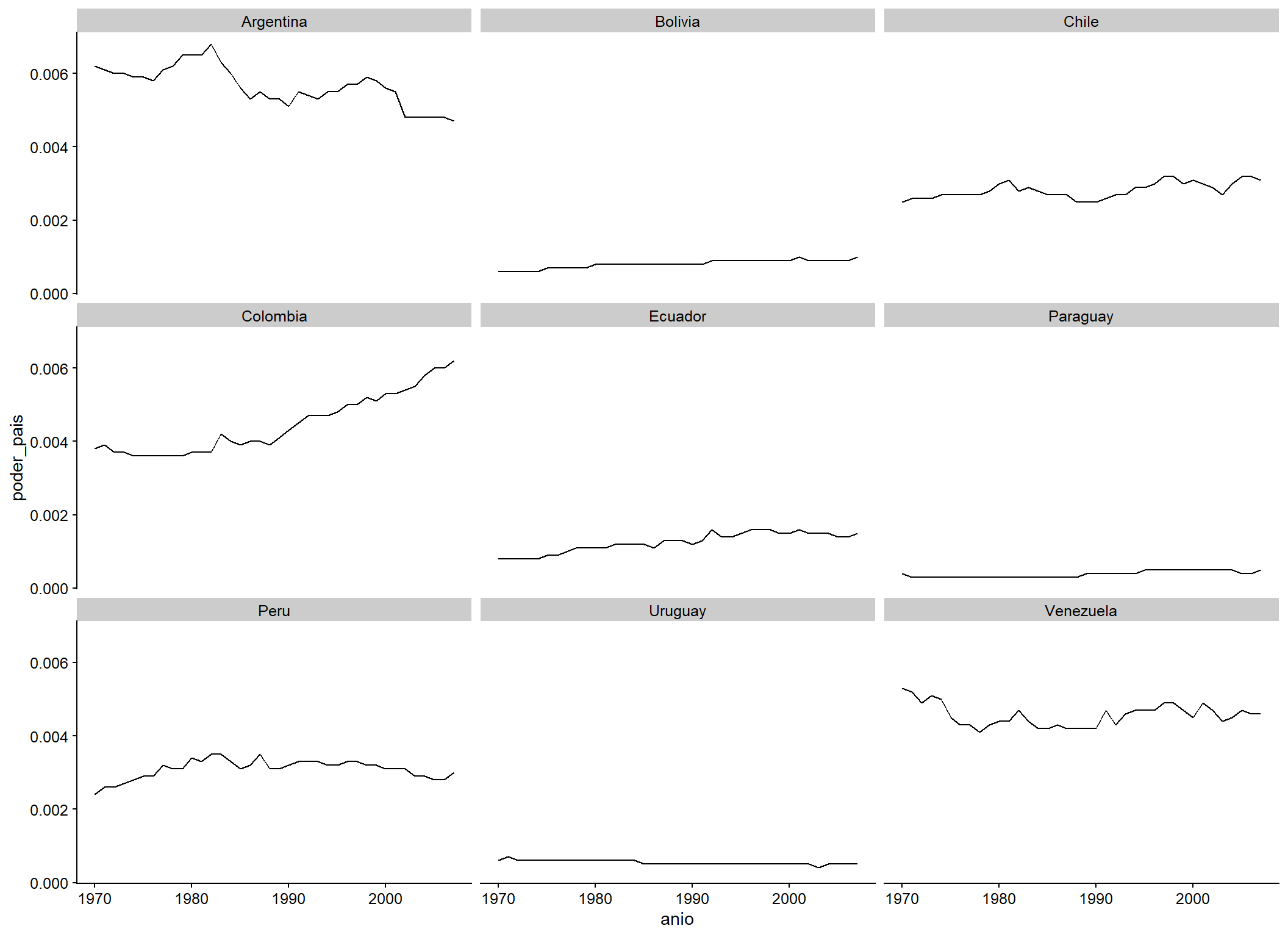

Figura 3.12: Evolución del índice CINC en el tiempo para los países de América del Sur

Ejercicio 7A. Usando la base de datos del capítulo de MCO (Latin America Welfare Dataset, 1960-2014, Huber et al. 2006), grafica el comportamiento del Índice de Gini (gini_slc) en América Latina a lo largo del tiempo.

7.3 Modelización de la variación a nivel de grupo

Un panel de datos (o TSCS) contendrá datos para N unidades en T momentos. En este capítulo, N son países, pero en tu base de datos podrían ser partidos políticos, países, legisladores o cualquier otra unidad de observación de interés. En este capítulo, T son años, pero en tu base de datos podrían ser meses, semestres o décadas. Obviamente necesitamos regularidad en la periodización. Si tenemos años, es importante que el panel no mezcle dos unidades temporales diferentes (por ejemplo, datos por año y década).

Si nuestra base de datos no contiene valores perdidos, diremos que nuestro panel está balanceado, ya que tenemos la misma cantidad de Ts para cada N. Si, por el contrario, hay valores perdidos, nuestro panel no estará balanceado.³⁵. Al tener datos que varían a lo largo del tiempo y/o entre los individuos, nuestro modelo tendrá más información que en los modelos de corte transversal, obteniendo así estimadores más eficientes. Los datos de panel le permitirán controlar por medio de las heterogeneidades existentes entre las unidades que no varían en el tiempo, y reducir el sesgo de las variables omitidas, así como testear la hipótesis del comportamiento de las observaciones en el tiempo.

Algunas de sus variables serán constantes a lo largo del tiempo, es decir, no variarán en T, sino en N. Por ejemplo, la superficie geográfica de un país o la distancia a otro país no cambiará en condiciones normales (podría variar si hubiera una guerra y las fronteras nacionales cambiaran, por ejemplo). En el caso de las personas, algunos atributos como la nacionalidad o el género tienden a permanecer iguales a lo largo del tiempo. En la ciencia política, normalmente tendremos más Ns que Ts en nuestro panel, aunque puede haber excepciones. Nos interesarán dos tipos de efectos sobre la variable dependiente: efectos sobre \(Y\) que varían en \(t\) pero no en \(i\), y efectos que varían en \(i\) pero no en \(t\). Los efectos que varían en \(i\) y en \(t\) se consideran en el término de error \(\epsilon_i,_t\). Si ignoramos estos efectos, obtendremos coeficientes sesgados. ¡Observémoslo gráficamente!

Este es un modelo en el que ignoramos la existencia de once países en la muestra, y tratamos cada observación como independiente. Por eso lo llamamos de pooled (agregado).

pooled <- lm(voto ~ poder_pais, data = eeuu_latam)

summary(pooled)
## 
## Call:
## lm(formula = voto ~ poder_pais, data = eeuu_latam)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.3194 -0.1465 -0.0538  0.0957  0.5657 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    0.380      0.012   31.67   <2e-16 ***
## poder_pais    -3.564      1.473   -2.42    0.016 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.19 on 378 degrees of freedom
## Multiple R-squared:  0.0152, Adjusted R-squared:  0.0126 
## F-statistic: 5.85 on 1 and 378 DF,  p-value: 0.016

Este es un modelo en el que incorporamos un intercepto a cada país, asumiendo que nuestras variables varían entre las observaciones

manual_fe <- lm(voto ~ poder_pais + factor(pais), data = eeuu_latam)

summary(manual_fe)
## 
## Call:
## lm(formula = voto ~ poder_pais + factor(pais), data = eeuu_latam)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -0.3129 -0.1332 -0.0384  0.1002  0.5908 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)    
## (Intercept)             0.8145     0.0768   10.60  < 2e-16 ***
## poder_pais            -78.8200    12.5378   -6.29  9.2e-10 ***
## factor(pais)Bolivia    -0.3637     0.0738   -4.93  1.2e-06 ***
## factor(pais)Brazil      1.3909     0.2313    6.01  4.4e-09 ***
##  [ reached getOption("max.print") -- omitted 7 rows ]
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.18 on 369 degrees of freedom
## Multiple R-squared:  0.125,  Adjusted R-squared:  0.101 
## F-statistic: 5.25 on 10 and 369 DF,  p-value: 3.18e-07

Si extraemos los valores predichos de este modelo podemos comparar la diferencia que genera en el coeficiente poder_pais proporcionando esta información al modelo:

eeuu_latam <- eeuu_latam %>%
  mutate(hat_fe = fitted(manual_fe))

Como se puede observar en la siguiente figura, el coeficiente del modelo combinado para poder_pais es de -3.56, mientras que para el modelo que tiene en cuenta la heterogeneidad de las unidades es de -78.8. Esta corrección se logra incorporando un intercepto para cada observación. En la figura se muestra la pendiente de cada país una vez añadidos los dummies, y la pendiente es menor cuando hacemos una regresión agregada (línea negra). La especificidad que incluyen los interceptos para cada observación se conoce como modelo de efectos fijos, y es el modelo más común para modelar datos en panel.

ggplot(data = eeuu_latam, aes(x = poder_pais, y = hat_fe, 
                              label = pais, group = pais)) +
  geom_point() +
  # add pais-specific lines
  geom_smooth(method = "lm", se = F, color = "black") +
  # add pooled line
  geom_smooth(mapping = aes(x = poder_pais, y = hat_fe), inherit.aes = F,
              method = "lm", se = T, color = "black", linetype = "dashed") +
  # label lines
  geom_text(
    data = eeuu_latam %>% 
      group_by(pais) %>% 
      top_n(1, poder_pais) %>% 
      slice(1),
    mapping = aes(label = pais), vjust = 1
  )

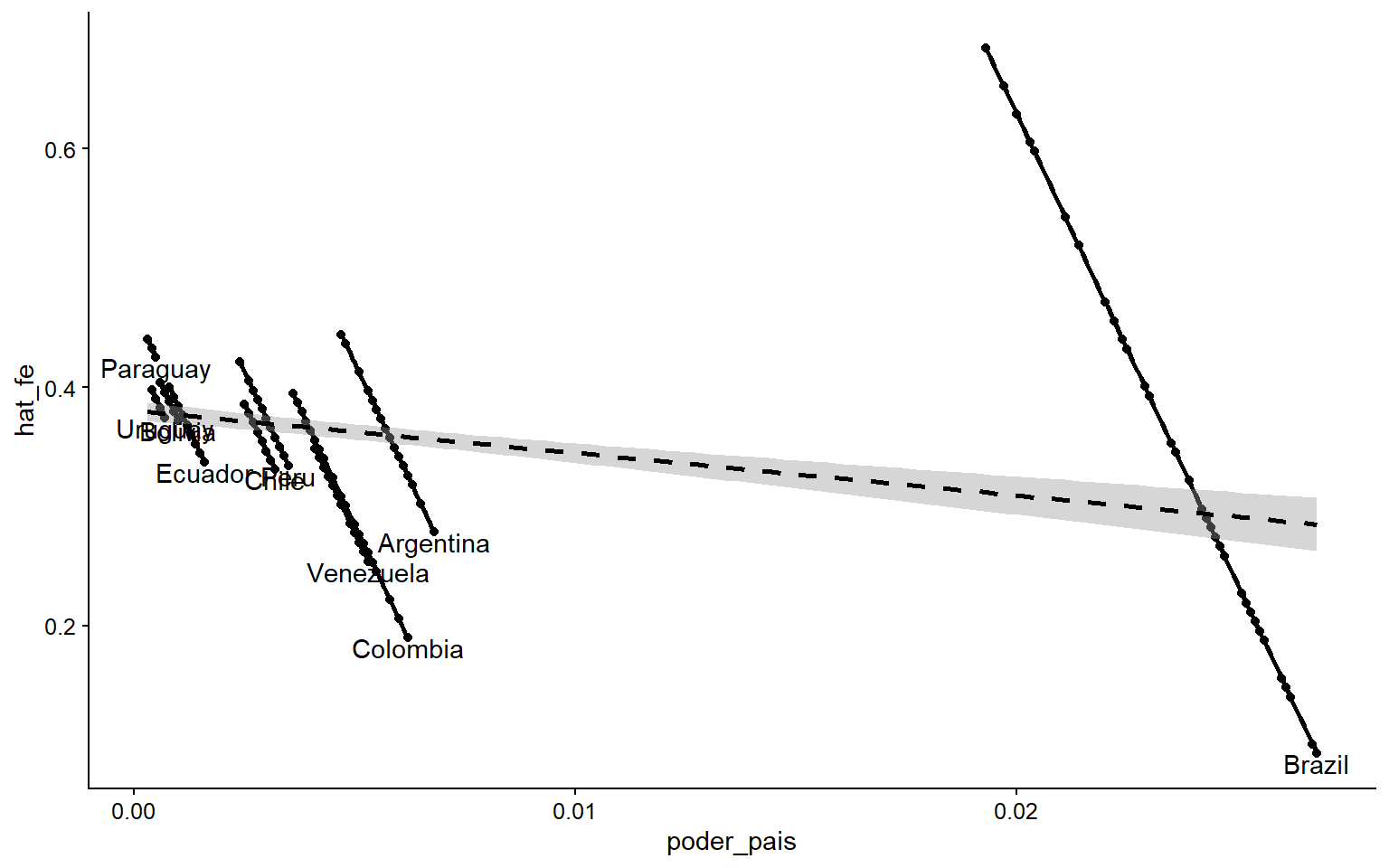
Figura 3.16: Al añadir los dummies de países, la pendiente de la relación lineal cambia sustancialmente

7.4 Efectos fijos vs. efectos aleatorios

En las ciencias políticas, las dos especificaciones para la modelización de la variación entre grupos en los datos de panel son modelos de efectos fijos o aleatorios. Todavía no está claro para los investigadores aplicados cuándo debe utilizarse uno u otro. Una buena discusión sobre este tema es presentada por Clark and Linzer (2015). Los modelos de efectos fijos añaden una variable dicotómica (dummy) para cada unidad. Los modelos de efectos aleatorios suponen que la variación entre unidades sigue una distribución de probabilidad, típicamente normal, con parámetros estimados a partir de los datos.

El argumento index = es necesario para informar cuál es nuestro N y cuál es nuestro T, en este caso c("codigo", "anio"). plm, por defecto, genera modelos de efectos fijos, por lo que no necesitamos usar la opción model. Si comparas el modelo fe que generaremos con el modelo manual_fe, notará que el coeficiente de poder_pais es el mismo.

library(plm)

fe <- plm(voto ~ poder_pais, data = eeuu_latam, index = c("codigo", "anio"))

summary(fe)
## Oneway (individual) effect Within Model
## 
## Call:
## plm(formula = voto ~ poder_pais, data = eeuu_latam, index = c("codigo", 
##     "anio"))
## 
## Balanced Panel: n = 10, T = 38, N = 380
## 
## Residuals:
##    Min. 1st Qu.  Median 3rd Qu.    Max. 
## -0.3129 -0.1332 -0.0384  0.1002  0.5908 
## 
## Coefficients:
##            Estimate Std. Error t-value Pr(>|t|)    
## poder_pais    -78.8       12.5   -6.29  9.2e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    13.5
## Residual Sum of Squares: 12.2
## R-Squared:      0.0967
## Adj. R-Squared: 0.0723
## F-statistic: 39.5215 on 1 and 369 DF, p-value: 9.17e-10

Si quieres obtener los efectos fijos de los interceptos para compararlos con el modelo manual, necesitas usar la función fixef().

fixef(fe, type = "dfirst")
##      2      3      4      5      6      8      9     10     11 
## -0.364  1.391 -0.232 -0.136 -0.352 -0.350 -0.204 -0.143 -0.385

Por el contrario, para los efectos aleatorios necesitamos especificar specify model = "random".

re <- plm(voto ~ poder_pais, data = eeuu_latam, 
          index = c("codigo", "anio"), model = "random")

summary(re)
## Oneway (individual) effect Random Effect Model 
##    (Swamy-Arora's transformation)
## 
## Call:
## plm(formula = voto ~ poder_pais, data = eeuu_latam, model = "random", 
##     index = c("codigo", "anio"))
## 
## Balanced Panel: n = 10, T = 38, N = 380
## 
## Effects:
##                   var std.dev share
## idiosyncratic 0.03311 0.18195  0.99
## individual    0.00017 0.01304  0.01
## theta: 0.0853
## 
## Residuals:
##    Min. 1st Qu.  Median 3rd Qu.    Max. 
## -0.3149 -0.1449 -0.0551  0.0974  0.5653 
## 
## Coefficients:
##             Estimate Std. Error z-value Pr(>|z|)    
## (Intercept)   0.3814     0.0131   29.10   <2e-16 ***
## poder_pais   -3.7487     1.6057   -2.33     0.02 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    13.9
## Residual Sum of Squares: 13.7
## R-Squared:      0.0142
## Adj. R-Squared: 0.0116
## Chisq: 5.45058 on 1 DF, p-value: 0.0196

7.4.1 Test de Hausman

El Test de Hausman suele utilizarse para decidir si es preferible estimar el modelo con efectos fijos o con modelos aleatorios. En este test se asume que el modelo de efectos fijos es consistente para los parámetros verdaderos, y el modelo de efectos aleatorios es una especificación eficiente de los efectos individuales bajo el supuesto de que son aleatorios y siguen una distribución normal. Se supone que el modelo de efectos fijos calcula siempre el estimador consistente, mientras que el modelo de efectos aleatorios calculará el estimador que es consistente y eficiente bajo \(H_0\). El comando para realizar esta prueba es phtest, que es parte del paquete plm.

phtest(fe, re)
## 
##  Hausman Test
## 
## data:  voto ~ poder_pais
## chisq = 36, df = 1, p-value = 2e-09
## alternative hypothesis: one model is inconsistent

Bajo la especificación actual, nuestra hipótesis inicial de que los efectos a nivel individual son modelados adecuadamente con un modelo de efectos aleatorios es claramente rechazada, con un valor p inferior al umbral de 0,05. En este caso, debemos quedarnos con el modelo de efectos fijos.

Ejercicio 7B. Utilice la base de datos del capítulo de la MCO (Latin America Welfare Dataset, 1960-2014, de Evelyne Huber y John D. Stephens) para estimar un modelo de efectos fijos y otro de efectos aleatorios en el que su variable dependiente sea el índice de Gini (gini_slc) y la variable independiente sea el gasto en educación (gasto_educ). A continuación, realice un test de especificación de Hausman.

7.5 Testeando raíces unitarias

Muchas series temporales de datos políticos exhiben un comportamiento con tendencias temporales, es decir, un comportamiento no estacionario en la media. Sin embargo, la existencia no estacionalidad no siempre se testea. Esto no es un detalle menor, ya que la no estacionalidad puede conducir fácilmente a regresiones espurias, y hay serias posibilidades de obtener resultados falsamente significativos. Dos procedimientos comunes de eliminación de tendencias temporales, también llamado de “desestacionalización” son las transformaciones de las variables a primeras diferencias y la inclusión como control de tendencias temporales. Un modelo de datos de panel dinámico es aquel que contiene (al menos) una variable dependiente con un lag (una variable desfazada en el tiempo, por ejemplo en t-1) y un modelo de primeras diferencias es aquel en el que tanto las variables dependientes como las independientes se expresan como \(\Delta\), es decir, como \(X_t-(X_{t-1})\). En cierto sentido, una variable dependiente desfazada introduce el efecto del pasado en el modelo. Después de incluirlo, la variable dependiente es influenciada no sólo por el valor actual de la variable independiente (\(X_t\)), sino también por los valores de la variable independiente en el pasado, (\(X_{t-1}\), \(X_{t-2}\), etc.).

Exploremos nuestros datos y testeemos las raíces unitarias en nuestra especificación de efectos fijos.

fe <- plm(voto ~ poder_pais, data = eeuu_latam, index = c("codigo", "anio"))

summary(fe)
## Oneway (individual) effect Within Model
## 
## Call:
## plm(formula = voto ~ poder_pais, data = eeuu_latam, index = c("codigo", 
##     "anio"))
## 
## Balanced Panel: n = 10, T = 38, N = 380
## 
## Residuals:
##    Min. 1st Qu.  Median 3rd Qu.    Max. 
## -0.3129 -0.1332 -0.0384  0.1002  0.5908 
## 
## Coefficients:
##            Estimate Std. Error t-value Pr(>|t|)    
## poder_pais    -78.8       12.5   -6.29  9.2e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    13.5
## Residual Sum of Squares: 12.2
## R-Squared:      0.0967
## Adj. R-Squared: 0.0723
## F-statistic: 39.5215 on 1 and 369 DF, p-value: 9.17e-10

Si exploramos cuán altamente correlacionadas están nuestras variables dependientes e independientes con nuestra variable de tiempo, podríamos tener una idea de cómo tendencias en el tiempo pueden sesgar nuestros hallazgos. La figura que creamos con ggcorrplot muestra que poder_pais tiene una correlación positiva muy fuerte con anio, mientras que la variable anio tiene una correlación muy negativa con la variable voto.

library(ggcorrplot)

corr_selected <- eeuu_brasil %>% 
  select(anio, poder_pais, voto) %>% 
  # calcular la matriz de correlación y redondear a un decimal
  cor(use = "pairwise") %>% 
  round(1)
  
ggcorrplot(corr_selected, type = "lower", lab = T, show.legend = F)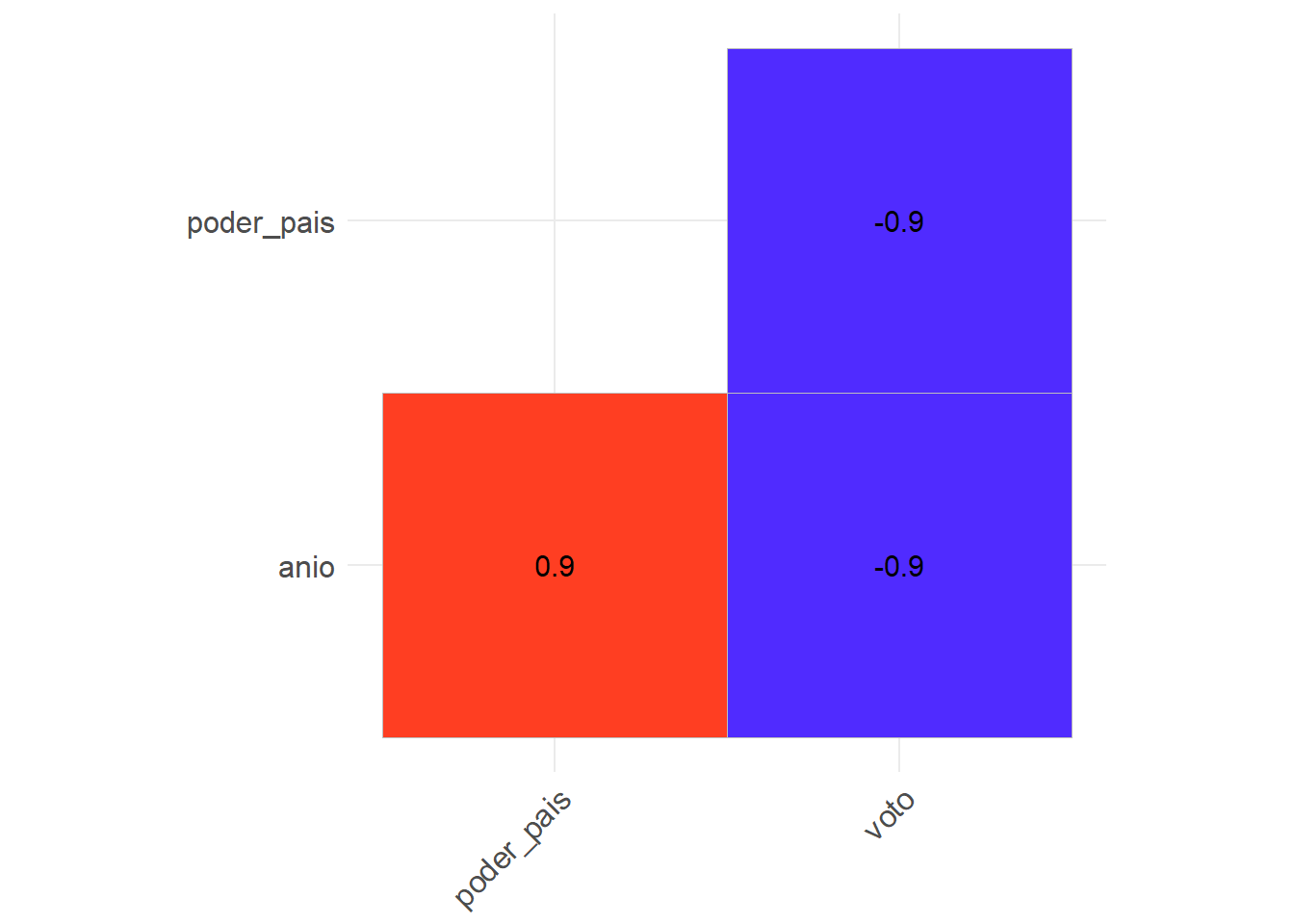

Figura 3.22: Correlación con la variable de tiempo

Esta es una advertencia, ya que podría ser que el poder_pais no explique el anio después de todo, lo que haría que nuestros hallazgos iniciales fueran espurios. Para diagnosticar raíces unitarias usaremos la función purtest. Hay múltiples tests disponibles, cada uno con diferentes especificaciones, por lo tanto, revisar todas sus diferencias excede el propósito de este capítulo. Utilizaremos dos, que son adecuadas para nuestro objetivo de detectar raíces unitarias en nuestras variables dependientes e independientes. Estos son los de Levin, Lin, and James Chu (2002) y Im, Pesaran, and Shin (2003).

# opción del test de Levin et al. (2002)
purtest(voto ~ 1, data = eeuu_latam, 
        index = c("pais", "anio"), pmax = 10, test = "levinlin", 
        lags = "AIC", exo = "intercept")
## 
##  Levin-Lin-Chu Unit-Root Test (ex. var.: Individual Intercepts)
## 
## data:  voto ~ 1
## z = -2, p-value = 0.03
## alternative hypothesis: stationarity

# opción del test de Im et al. (2003)
purtest(voto ~ 1, data = eeuu_latam, 
        index = c("pais", "anio"), pmax = 10, test = "ips", 
        lags = "AIC", exo = "intercept")
## 
##  Im-Pesaran-Shin Unit-Root Test (ex. var.: Individual
##  Intercepts)
## 
## data:  voto ~ 1
## Wtbar = -1, p-value = 0.1
## alternative hypothesis: stationarity

En este caso, sólo uno de los modelos, el de ips, indica la existencia de raíces unitarias. Aunque la evidencia no es absoluta, vale la pena corregir las posibles raíces unitarias en anio. Ahora, observemos nuestra variable dependiente.

# test de Levin et al. (2002)
purtest(poder_pais ~ 1, data = eeuu_latam, 
        index = c("pais", "anio"), pmax = 10, test = "levinlin", 
        lags = c("AIC"), exo = c("intercept"))
## 
##  Levin-Lin-Chu Unit-Root Test (ex. var.: Individual Intercepts)
## 
## data:  poder_pais ~ 1
## z = -0.6, p-value = 0.3
## alternative hypothesis: stationarity

# test de Im et al. (2003)
purtest(poder_pais ~ 1, data = eeuu_latam, 
        index = c("pais", "anio"), pmax = 10, test = "ips", 
        lags = "AIC", exo = "intercept")
## 
##  Im-Pesaran-Shin Unit-Root Test (ex. var.: Individual
##  Intercepts)
## 
## data:  poder_pais ~ 1
## Wtbar = -0.4, p-value = 0.4
## alternative hypothesis: stationarity

En este caso, ambos modelos son claros al indicar las raíces unitarias en la variable de poder de los países. Intentaremos resolver el problema especificando dos modelos, uno dinámico y otro con primeras diferencias. En este capítulo no tenemos la extensión para cubrir cuál es el preferible en cada situación, por lo que asumiremos que ambos son igualmente válidos. Para especificar estos modelos, primero tenemos que aprender a crear variables rezagadas (t-1, t-2, etc.), variables prospectivas (t+1, t+2, etc.) y primeras diferencias (\(\Delta\)).

7.5.1 Creación de variables rezagadas (lags) y variables prospectivas (leads)

La siguiente porción de código crea variables que probablemente necesitemos. Primero, clasificamos (arrange) nuestro panel de acuerdo a nuestros Ns y Ts. Este es un paso importante para que la base de datos no confunda nuestras observaciones. Luego, las agrupamos según nuestro N, en este caso pais. Finalmente, creamos las variables. Después de la función (por ejemplo, lag) especificamos que es un rezago en relación a t-1. Para un rezago mayor, cambiaríamos el 1 por otro valor en el código. Hemos creado una de cada tipo para que sepas cómo hacerlo, pero no usaremos aquí la variable voto_lead1.

eeuu_latam <- eeuu_latam %>%
  arrange(pais, anio) %>% 
  group_by(pais) %>% 
  mutate(voto_lag1 = dplyr::lag(voto, 1),
         voto_lead1 = dplyr::lead(voto, 1),
         voto_diff1 = c(NA, diff(voto))) %>% 
  ungroup()

Ahora hacemos lo mismo con la variable poder_pais. Crearemos un rezago (t-1) y la diferencia (\(Delta\))

eeuu_latam <- eeuu_latam %>%
  arrange(pais, anio) %>% 
  group_by(pais) %>% 
  mutate(poder_pais_lag1 = dplyr::lag(poder_pais, 1),
         poder_pais_diff1 = c(NA, diff(poder_pais))) %>% 
  ungroup()

Modelo dinámico

Nuestro modelo dinámico incluirá la variable rezagada de la variable dependiente. Así, voto_lag1 es un predictor del voto en el presente. Notarán que, al incluir esta variable, la hipótesis de Amorim Neto de que cuanto mayor sea el poder del país, menor será la convergencia de los votos en la AGNU, queda sin sustento empírico. Ojalá esto sea una advertencia de que es esencial que cuando utilices datos en panel que siempre hagas este tipo de tests.

fe_lag <- plm(voto ~ voto_lag1 + poder_pais, data = eeuu_latam,
              index = c("codigo", "anio"))
summary(fe_lag)
## Oneway (individual) effect Within Model
## 
## Call:
## plm(formula = voto ~ voto_lag1 + poder_pais, data = eeuu_latam, 
##     index = c("codigo", "anio"))
## 
## Balanced Panel: n = 10, T = 37, N = 370
## 
## Residuals:
##     Min.  1st Qu.   Median  3rd Qu.     Max. 
## -0.20668 -0.04013 -0.00833  0.02616  0.28549 
## 
## Coefficients:
##            Estimate Std. Error t-value Pr(>|t|)    
## voto_lag1    0.8912     0.0218   40.90   <2e-16 ***
## poder_pais  -3.0418     5.7186   -0.53      0.6    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    12.3
## Residual Sum of Squares: 1.98
## R-Squared:      0.839
## Adj. R-Squared: 0.834
## F-statistic: 934.399 on 2 and 358 DF, p-value: <2e-16

Modelo de primeras diferencias Lo mismo ocurre cuando se prueban los modelos con las primeras diferencias, por lo que la hipótesis del capítulo se queda sin sustento.

fe_diff <- plm(voto_diff1 ~ poder_pais_diff1, data = eeuu_latam,
               index = c("codigo", "anio"))

summary(fe_diff)
## Oneway (individual) effect Within Model
## 
## Call:
## plm(formula = voto_diff1 ~ poder_pais_diff1, data = eeuu_latam, 
##     index = c("codigo", "anio"))
## 
## Balanced Panel: n = 10, T = 37, N = 370
## 
## Residuals:
##     Min.  1st Qu.   Median  3rd Qu.     Max. 
## -0.24860 -0.04107 -0.00426  0.03102  0.27316 
## 
## Coefficients:
##                  Estimate Std. Error t-value Pr(>|t|)
## poder_pais_diff1     12.6       15.3    0.83     0.41
## 
## Total Sum of Squares:    2.13
## Residual Sum of Squares: 2.12
## R-Squared:      0.00189
## Adj. R-Squared: -0.0259
## F-statistic: 0.68067 on 1 and 359 DF, p-value: 0.41

Por último, comparemos el modelo que no considera las raíces unitarias (fe) con el que lo corrige (fe_lag) a través de la prueba Wooldridge de errores AR(1) en los modelos de paneles de efectos fijos:

pwartest(fe)
## 
##  Wooldridge's test for serial correlation in FE panels
## 
## data:  fe
## F = 4437, df1 = 1, df2 = 368, p-value <2e-16
## alternative hypothesis: serial correlation

pwartest(fe_lag)
## 
##  Wooldridge's test for serial correlation in FE panels
## 
## data:  fe_lag
## F = 0.7, df1 = 1, df2 = 358, p-value = 0.4
## alternative hypothesis: serial correlation

Obviamente hemos cubierto estos contenidos sin entrar en muchos detalles o explicaciones. Uno podría escribir un libro entero sobre este capítulo. Para aprender más sobre este tema, sería genial si pudiera leer las lecturas sugeridas al principio de este capítulo, especialmente Beck y Katz (2011)³⁶.

Ejercicio 7C. Utiliza el Latin America Welfare Dataset para crear variables rezagadas en t-1 y t-10 del Índice Gini (gini_slc). Incorpore ambas variables en tu modelo y diagnostica las raíces unitarias.

7.6 Errores estándar robustos corregidos para panel

7.6.1 Errores estándar robustos

Quizás has utilizado Stata en algún momento para hacer análisis de datos en panel, o tal vez uno de tus coautores quiere replicar tus resultados en Stata. Si deseas reportar errores estándar robustos equivalentes a los de la opción “robust” de Stata, usted necesita calcularlos con coeftest y definir type"sss", que corresponde a la misma corrección de muestra pequeña para datos de panel que hace Stata.

library(lmtest)

Si quisieras hacerlo para el modelo original de efectos fijos (fe) puedes con la siguiente línea de código:

coeftest(fe, vcov. = function(x){vcovHC(x, type = "sss")}) 
## 
## t test of coefficients:
## 
##            Estimate Std. Error t value Pr(>|t|)    
## poder_pais    -78.8       19.4   -4.06    6e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Y para compararlos con los errores estándar originales:

summary(fe)
## Oneway (individual) effect Within Model
## 
## Call:
## plm(formula = voto ~ poder_pais, data = eeuu_latam, index = c("codigo", 
##     "anio"))
## 
## Balanced Panel: n = 10, T = 38, N = 380
## 
## Residuals:
##    Min. 1st Qu.  Median 3rd Qu.    Max. 
## -0.3129 -0.1332 -0.0384  0.1002  0.5908 
## 
## Coefficients:
##            Estimate Std. Error t-value Pr(>|t|)    
## poder_pais    -78.8       12.5   -6.29  9.2e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Total Sum of Squares:    13.5
## Residual Sum of Squares: 12.2
## R-Squared:      0.0967
## Adj. R-Squared: 0.0723
## F-statistic: 39.5215 on 1 and 369 DF, p-value: 9.17e-10

También es posible que quieras calcular los errores estándar corregidos para panel, equivalentes al comando xtpcse de Stata. Estos errores estándar se han popularizado en la ciencia política desde el clásico artículo de Beck y Katz (1995)³⁷. En 2011 se publicó un paquete para calcularlos en R³⁸. En el artículo, los autores explican que estos errores estándar son útiles para aquellos que trabajan con paneles de “estados o naciones”:

“Los datos de series temporales transversales (TSCS) se caracterizan por tener observaciones repetidas a lo largo del tiempo, como puede ser datos de estados o naciones a lo largo de los años. Los datos TSCS típicamente sufren de correlación contemporánea entre las unidades y de heteroscedasticidad a nivel de unidad, haciendo que la inferencia de los errores estándar producidos por MCO sea incorrecta. Los errores estándar corregidos para panel (PCSE) dan cuenta de estas desviaciones en los errores y permiten una mejor inferencia de los modelos lineales estimados a partir de datos de tipo TSCS.”

Para usar los errores estándar corregidos para Panel (PCSE) necesitas usar la opción vcov = "vcovBK" dentro de la función coeftest(). Debes fijar el argumento cluster = "time".

coeftest(fe, vcov = vcovBK, type = "HC1", cluster = "time")
## 
## t test of coefficients:
## 
##            Estimate Std. Error t value Pr(>|t|)    
## poder_pais    -78.8       11.3   -6.96  1.6e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Voilá!

Hasta este punto, hemos cubierto las funciones básicas que necesitas tener en cuenta para analizar los datos de tu panel. Para ampliar tus conocimientos, consulta la bibliografía recomendada al principio del capítulo. Esperamos que este capítulo te haya resultado útil.

Ejercicio 7D. En el modelo que estimaste en el ejercicio anterior, calcula los errores estándar corregidos para panel.

E-mail: furdinez@uc.cl↩︎
Este ejemplo fue tomado de un curso de Mine Cetinkaya, su sitio web tiene más recursos útiles que vale la pena ver↩︎
En el capítulo de manejo avanzado de datos aprenderá cómo imputar los valores perdidos↩︎
Beck and Katz (2011)↩︎
Beck and Katz (1995)↩︎
Bailey and Katz (2011)↩︎