Capítulo 14 Análisis de redes
Andrés Cruz57
Lecturas sugeridas
Newman, M. (2018). Networks: An Introduction (2nd ed). New York: Oxford University Press.
Scott, J. (2013). Social Network Analysis (3rd ed.). London: Sage Publications.
Los paquetes que necesitas instalar
tidyverse(Wickham 2019b),paqueteadp(Urdinez and Cruz 2020),tidygraph(Pedersen 2020b),ggraph(Pedersen 2020a),ggcorrplot(Kassambara 2019).
14.1 Introducción
No es exagerado decir que en la política todo está conectado a todo. Por ejemplo, consideremos el caso de los legisladores. Las conexiones son obvias: partidos, coaliciones, comisiones, lazos familiares, escuelas. Para entender mejor estas relaciones enredadas, una de las herramientas de la caja de herramientas de los científicos sociales es el análisis de redes. Las redes pueden reconocer que todo está conectado con todo lo demás y dar pistas sobre cómo se construyen esas conexiones. Las redes no sólo nos permiten visualizar estas conexiones de una manera convincente, sino que también nos permiten medir cuán cercanos son los actores. En este capítulo aprenderás los fundamentos del análisis de redes con R, principalmente usando los paquetes tidygraph y ggraph, que abordan el análisis de redes desde los preceptos del tidyverse.
14.2 Conceptos básicos en una red
14.2.1 Nodos y enlaces
Hay dos conceptos básicos que expresan una cierta situación en forma de red. Los nodos (a veces llamados actores) son las principales unidades de análisis: queremos entender cómo se relacionan entre sí. Los enlaces (a veces llamados conexiones) muestran cómo los nodos están conectados entre sí. Por ejemplo, entre los legisladores (los nodos), un posible enlace es “haber propuesto una ley juntos,” también llamado co-patrocinio.
Una red no es más que una serie de nodos conectados por enlaces, como se puede ver en la Figura 14.1. En cuanto al ejemplo anterior, podemos imaginar que dicha red gráfica conecta a los legisladores A, B, C y D según su copatrocinio de los proyectos w, x, y o z. Así, la red muestra que el legislador B ha presentado al menos un proyecto de ley con todos los demás legisladores de la red, mientras que el legislador D sólo ha presentado un proyecto de ley con B. Los legisladores A y C tienen dos enlaces de copatrocinio cada uno, formando un trío A-B-C.
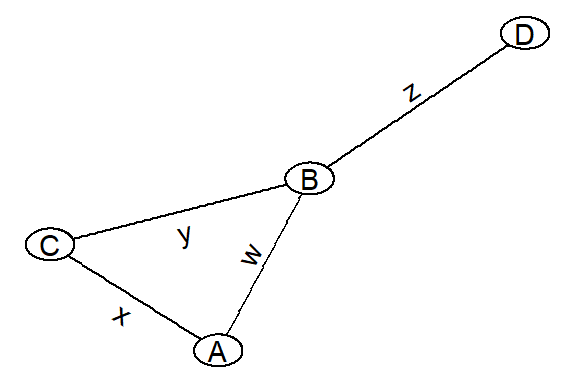
Figura 14.1: Diagrama de la red de copatrocinio de cuatro legisladores
14.2.2 Matriz de adyacencia
Aparte de una descripción visual, como la de la Figura 14.1, también es posible representar las redes como matrices adyacentes. La tabla 14.1 muestra la misma red que arriba, pero en formato de matriz. El “1” indica que existe un vínculo entre dos nodos (copatrocinio, en nuestro ejemplo), mientras que el 0 indica lo contrario. Observa cómo la diagonal de la matriz se rellena con ceros: es una convención útil para diferentes cálculos matemáticos. Además, este tipo de matriz para una red básica es simétrica: si sabemos que el nodo A está vinculado al nodo B, sabemos automáticamente que el nodo B está vinculado al nodo A.
| A | 0 | 1 | 1 | 0 |
| B | 1 | 0 | 1 | 1 |
| C | 1 | 1 | 0 | 0 |
| D | 0 | 1 | 0 | 0 |
14.2.3 Pesos y direcciones
La naturaleza de nuestros datos nos permite crear una red mucho más compleja que el ejemplo anterior. Específicamente, podemos añadir pesos y direcciones a los enlaces. Para empezar con los pesos, en nuestro ejemplo actual los legisladores están conectados si alguna vez han presentado un proyecto de ley juntos. Sin embargo, a menudo es interesante no sólo saber la existencia de una conexión entre dos actores, sino también la fuerza de esa conexión: no es lo mismo que dos legisladores hayan aceptado a regañadientes presentar un proyecto de ley juntos en una sola ocasión, ya que es que han presentado varios proyectos de ley juntos y son aliados políticos. Volvemos a la matriz de adyacencia, esta vez incluyendo los pesos. En este nuevo ejemplo, de la Tabla 14.2, los legisladores A y B han introducido nueve proyectos de ley juntos, mientras que todos los demás pares de legisladores conectados han introducido dos proyectos de ley juntos. Obsérvese cómo, por convención, la diagonal de la matriz permanece llena de ceros.
| A | 0 | 9 | 2 | 0 |
| B | 9 | 0 | 2 | 2 |
| C | 2 | 2 | 0 | 0 |
| D | 0 | 2 | 0 | 0 |
La segunda forma de añadir información adicional a los enlaces es añadiendo direcciones. En algunas legislaturas, los proyectos de ley tienen un autor principal (patrocinador), al que se unen otros legisladores (copatrocinadores). En estos casos, la red de copatrocinadores tendrá naturalmente una dirección: un legislador “patrocinará” a otro firmando su proyecto de ley, sin que esta relación sea necesariamente recíproca. Es posible incluir esta información en la red, como se muestra en Fowler (2006) para el Congreso de los Estados Unidos. Una matriz de adyacencia con direcciones y pesos se verá como la de la Tabla 14.3.
Nota que la matriz es ahora asimétrica, ya que hay más información sobre la relación de copatrocinio entre los legisladores.58. Mientras que el Legislador A patrocinó siete proyectos de ley del Legislador B, el Legislador B sólo reciprocó en dos proyectos de ley. Todos los demás copatrocinios registrados previamente implican la reciprocidad de un proyecto de ley.
| A | 0 | 7 | 1 | 0 |
| B | 2 | 0 | 1 | 1 |
| C | 1 | 1 | 0 | 0 |
| D | 0 | 1 | 0 | 0 |
14.3 Bases de datos de la red
Siguiendo el espíritu del ejemplo anterior, en este capítulo trabajaremos con datos sobre el copatrocinio de leyes en el Senado argentino. Utilizaremos datos de Alemán et al. (2009), específicamente para el año 1983, justo después del retorno de la democracia. Comencemos por cargar las bases de datos:
library(tidyverse)library(paqueteadp)
data("copatrocinio_arg")
data("senadores_arg")Podemos comprobar que nuestras bases de datos fueron cargadas correctamente con ls():
ls()## [1] "copatrocinio_arg" "senadores_arg"Tenemos dos bases de datos. La primera contiene información de los nodos. Cada legislador está asignado a una identificación única (a partir de 1), condición necesaria para el correcto funcionamiento del tidygraph. Además, tenemos otra información sobre los legisladores: nombre, provincia, partido y coalición política.
senadores_arg
## # A tibble: 46 x 4
## id_sen nombre_sen provincia bloque_politico
## <int> <chr> <chr> <chr>
## 1 1 RAMON A ALMENDRA SANTA CRUZ JUSTICIALISTA
## 2 2 JULIO AMOEDO CATAMARCA JUSTICIALISTA
## 3 3 RAMON A ARAUJO TUCUMAN JUSTICIALISTA
## # ... with 43 more rowsMientras tanto, nuestra segunda base de datos contiene información sobre los enlaces, en este caso, el copatrocinio de leyes entre los senadores. En esta base de datos, se registran los pesos y direcciones. Por lo tanto, tiene tres variables: dos variables de identificación (que vinculan las identificaciones de los senadores) y el número de leyes copatrocinadas en el par. Por ejemplo, la primera observación indica que el Legislador 1 firmó un proyecto de ley del Legislador 2.
copatrocinio_arg
## # A tibble: 217 x 3
## id_sen_desde id_sen_hacia n_copatrocinio
## <int> <int> <int>
## 1 1 2 1
## 2 1 9 1
## 3 1 30 1
## # ... with 214 more rowsUna vez que tengamos dos bases de datos, podemos unirlas en un solo objeto de tidygraph para empezar a trabajar con ellos:
library(tidygraph)
tg_copatrocinio_arg <- tbl_graph(nodes = senadores_arg, edges = copatrocinio_arg,
directed = T) # Nuestra red está dirigidaLos objetos del tidygraph unen nodos y enlaces que serán útiles en las siguientes operaciones:
tg_copatrocinio_arg
## # A tbl_graph: 46 nodes and 217 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 46 x 4 (active)
## id_sen nombre_sen provincia bloque_politico
## <int> <chr> <chr> <chr>
## 1 1 RAMON A ALMENDRA SANTA CRUZ JUSTICIALISTA
## 2 2 JULIO AMOEDO CATAMARCA JUSTICIALISTA
## 3 3 RAMON A ARAUJO TUCUMAN JUSTICIALISTA
## 4 4 ALFREDO L BENITEZ JUJUY JUSTICIALISTA
## 5 5 ANTONIO TOMAS BERHONGARAY LA PAMPA UCR
## 6 6 DEOLINDO FELIPE BITTEL CHACO JUSTICIALISTA
## # ... with 40 more rows
## #
## # Edge Data: 217 x 3
## from to n_copatrocinio
## <int> <int> <int>
## 1 1 2 1
## 2 1 9 1
## 3 1 30 1
## # ... with 214 more rowsPodemos editar el contenido de cualquiera de las dos bases de datos, activando cualquiera de sus nodos o enlaces con activate(). Vamos a crear dos variables que serán de utilidad más adelante. Primero, una variable binaria para el copatrocinio usando if_else(), llamada “d_copatrocinio.” Segundo, una variable invertida para los pesos (número de proyectos de ley), que nombraremos “n_copatrocinio_inv.”
tg_copatrocinio_arg <- tg_copatrocinio_arg %>%
activate("edges") %>% # o "nodos" si quieres editar esa base de datos
mutate(d_copatrocinio = if_else(n_copatrocinio >= 1, 1, 0),
n_copatrocinio_inv = 1 / n_copatrocinio)Ahora los bordes se activan y se muestran primero:
tg_copatrocinio_arg
## # A tbl_graph: 46 nodes and 217 edges
## #
## # A directed simple graph with 1 component
## #
## # Edge Data: 217 x 5 (active)
## from to n_copatrocinio d_copatrocinio n_copatrocinio_inv
## <int> <int> <int> <dbl> <dbl>
## 1 1 2 1 1 1
## 2 1 9 1 1 1
## 3 1 30 1 1 1
## 4 1 34 1 1 1
## 5 1 36 3 1 0.333
## 6 1 37 1 1 1
## # ... with 211 more rows
## #
## # Node Data: 46 x 4
## id_sen nombre_sen provincia bloque_politico
## <int> <chr> <chr> <chr>
## 1 1 RAMON A ALMENDRA SANTA CRUZ JUSTICIALISTA
## 2 2 JULIO AMOEDO CATAMARCA JUSTICIALISTA
## 3 3 RAMON A ARAUJO TUCUMAN JUSTICIALISTA
## # ... with 43 more rows14.4 Presentación gráfica de una red
Teniendo nuestro objeto de red, una de las primeras acciones es graficarlo. ggraph (el paquete hermano de tidygraph) nos permitirá hacerlo usando el lenguaje de los gráficos, reutilizando conceptos y funciones que aprendiste de ggplot2 en capítulos anteriores.
library(ggraph)El diseño determina dónde se posicionarán los nodos en el plano. En general, una buena representación visual será capaz de revelar la estructura de la red, optimizar el uso del espacio y mostrar adecuadamente las relaciones entre los nodos (Pfeffer 2017).
Tal vez el algoritmo más común para el diseño gráfico es el de Fruchterman and Reingold (1991). Pertenece a la familia de los algoritmos de escalado de distancias, que funcionan bajo la premisa muy intuitiva de que los nodos más conectados deben estar más cerca unos de otros (Pfeffer 2017). Para usar el algoritmo FR en nuestra red, debemos empezar por generarlo con create_layout(). Nota que plantamos una semilla con set.seed(), ya que el procedimiento es iterativo y puede dar diferentes resultados en diferentes intentos.
set.seed(1)
layout_fr <- create_layout(tg_copatrocinio_arg, "fr", weights = n_copatrocinio)Habiendo creado el objeto con el diseño gráfico, procederemos a graficarlo. La función ggraph() será la base de nuestra cadena de comandos. A continuación, podemos usar geom_node_point() para mostrar los puntos del plano:
ggraph(layout_fr) +
geom_node_point(size = 5) +
theme_void() # un lienzo vacío para nuestra red
Figura 3.14: Red de copatrocinio en el Senado argentino (1983), nodos en el plano
La figura anterior no es muy informativa. Podemos proceder a añadir los enlaces con geom_edge_link(). Teniendo en cuenta que nuestra red está dirigida, añadiremos las flechas con el argumento arrow = arrow(length = unit(3, 'mm')) para fines ilustrativos (aunque típicamente pueden ser un poco confusas cuando se buscan patrones generales).
ggraph(layout_fr) +
geom_edge_link(arrow = arrow(length = unit(3, 'mm')),
color = "lightgrey") +
geom_node_point(size = 5) +
theme_void()
Figura 3.15: Red de copatrocinio en el Senado argentino (1983), con nodos y enlaces
Ejercicio 14A. Prueba la función
geom_edge_arc()en lugar degeom_edge_link(). ¿Cuál es la diferencia? ¿Qué visualización crees que es más clara?
Debemos recordar que nuestra red tiene pesos. Esto se tuvo en cuenta en el diseño gráfico cuando usamos el argumento weights = n_copatrocinio para create_layout(). Podemos incorporar esta información explícitamente en nuestros enlaces gráficos, usando el ahora familiar argumento mapping = aes() en nuestra geom. En este caso, graficaremos la intensidad del color en los enlaces, usando el argumento alpha =:
ggraph(layout_fr) +
geom_edge_link(mapping = aes(alpha = n_copatrocinio)) +
geom_node_point(size = 5) +
theme_void()
Figura 3.16: Red de copatrocinio en el Senado argentino (1983), vínculos con opacidad
El gráfico anterior muestra un grupo de legisladores particularmente cercano en la esquina superior izquierda. Podría ser interesante añadir información a los nodos de la red. En nuestra base de datos, conocemos el bloque político de cada legislador, así que usaremos esta información para editar los mapeos estéticos de geom_node_point():
ggraph(layout_fr) +
geom_edge_link(mapping = aes(alpha = n_copatrocinio)) +
geom_node_point(mapping = aes(color = bloque_politico, shape = bloque_politico), size = 5) +
scale_shape_manual(values = 15:18) + # Editar ligeramente las formas
theme_void()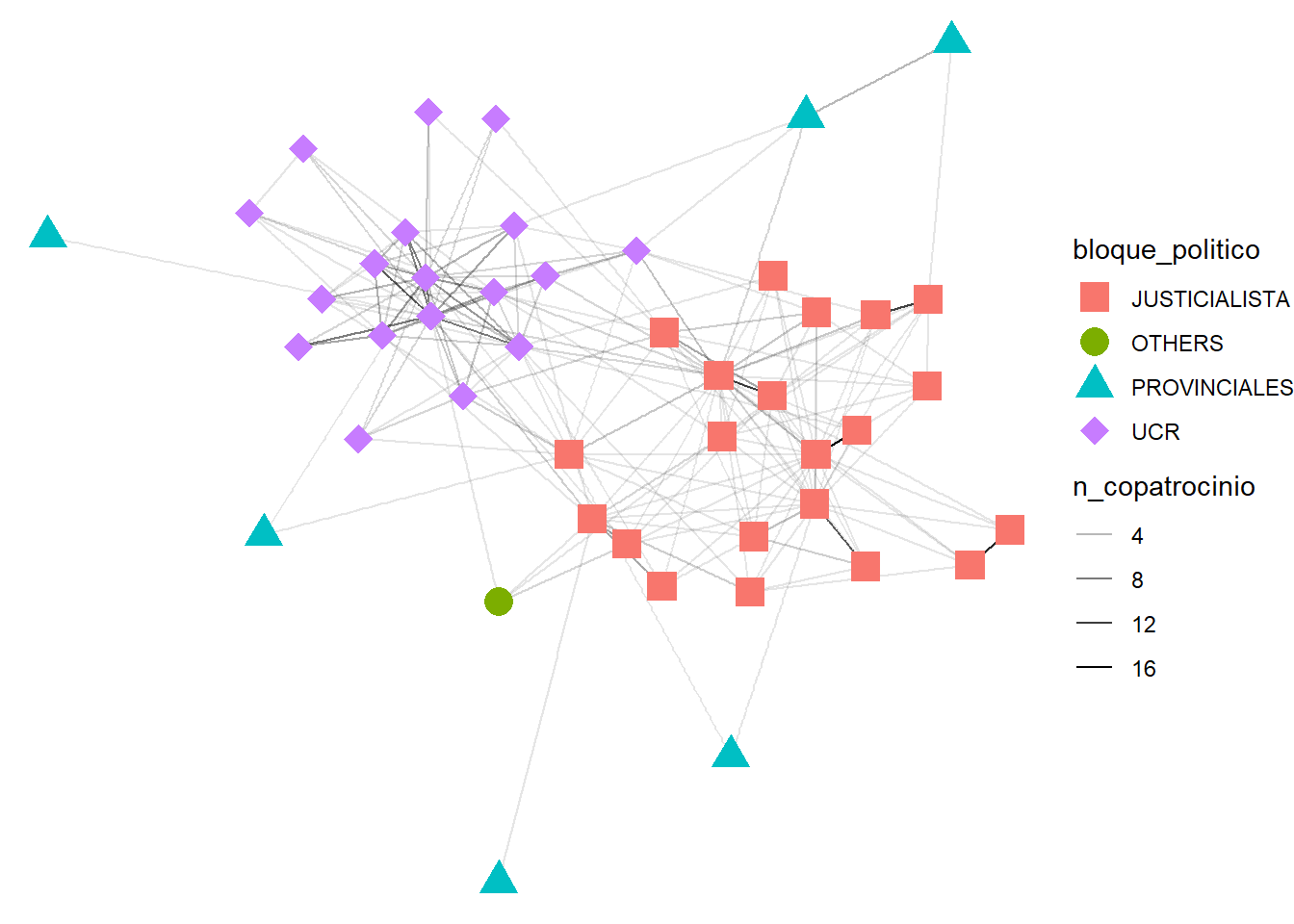
Figura 3.17: Red de copatrocinio en el Senado argentino (1983), versión completa
El patrón visual es particularmente claro. La red está dividida entre los dos grandes bloques políticos: el Justicialista y la Unión Cívica Radical (UCR). Los bloques provinciales más pequeños aparecen como satélites, con particulares vínculos de co-patrocinio en algunos proyectos. Una inspección gráfica de la red no es suficiente para sacar conclusiones.
Ejercicio 14B. Edita la base de datos del nodo en el objeto
tidygraph, con una columna que distinga los senadores metropolitanos (provinciasCAP FEDERALyBUENOS AIRES) del resto. Luego, usa esta nueva variable para colorear los nodos de la representación visual de la red.
14.5 Medidas de centralidad
Cuando se trata de datos de redes en las ciencias sociales, una de las primeras preguntas que hacemos tiene que ver con la influencia relativa de cada nodo. A menudo es relevante para nuestras preguntas de investigación descubrir figuras importantes, particularmente bien conectadas, etc. Sin embargo, el desarrollo de un estimador de centralidad no es del todo sencillo. En la literatura se han sugerido diferentes alternativas, que ponen de relieve diversas dimensiones de lo que intuitivamente podemos describir como “centralidad.” Ahora revisaremos las familias más comunes de estimadores: grado, centralidad eigenvectorial, entrelazado y cercanía. Para concluir, aprenderemos a aplicarlos en R, una tarea relativamente sencilla.
14.5.1 Grado
El grado es probablemente la medida más intuitiva de la centralidad: entenderemos que un nodo es central si está conectado a muchos otros nodos. De esta manera, el estimador de grados simplemente cuenta el número de conexiones de cada nodo. Dos variaciones requieren una mayor elaboración. En primer lugar, en una red con pesos, el grado también puede calcularse sumando todos los pesos de las conexiones existentes, lo que a veces se denomina la fuerza del nodo. Segundo, en redes dirigidas cada nodo tendrá dos medidas diferentes de grado: el in-degree (grado de entrada) y el out-degree (grado de salida). La primera contará las veces que los otros nodos se conectan al nodo en particular, mientras que la segunda registrará las veces que el nodo se conecta a otros.
14.5.2 Centralidad del eigenvector
Uno de los problemas más obvios de grado es que es ciego a la calidad de las conexiones, tal vez siendo demasiado poco refinado en algunos contextos. La centralidad del eigenvector y sus derivados consideran la idea de que “la gente importante conoce a la gente importante” (Patty and Penn 2016, 155). En otras palabras, no sólo importa el número de vínculos entre los nodos, sino también la importancia de los que componen esos vínculos.
Calcular la centralidad eigenvectorial de un nodo es un poco más complicado que obtener el grado, y su explicación algebraica está fuera del alcance de este capítulo (ver M. Newman 2018, 159–63). Intuitivamente, se debe tener en cuenta que es una medida algo tautológica, ya que “en lugar de conceder un punto por cada vecino de la red que tiene un nodo [como lo hace el grado], la centralidad eigenvectorial concede un número de puntos proporcional a las puntuaciones de centralidad de los vecinos.” (M. Newman 2018, 159, énfasis original).
El estimador crudo de centralidad de los vectores propios no funciona muy bien con las redes dirigidas, junto con algunos otros problemas (M. Newman 2018, 161–63). Uno de los estimadores alternativos más populares que refinan la centralidad de los vectores propios es el PageRank, el algoritmo utilizado por el motor de búsqueda de Google. En el contexto de las búsquedas en la web, “considera (1) el número de enlaces entrantes (es decir, los sitios que enlazan con tu sitio), (2) la calidad de los enlazantes (es decir, el PageRank de los sitios que enlazan con tu sitio), y (3) la propensión a enlazar de los enlazantes (es decir, el número de sitios a los que los enlazantes se vinculan)” (Hansen et al. 2019, 41). El PageRank puede ser usado en redes ponderadas y dirigidas, como nuestra red de ejemplo de copatrocinio en el Senado argentino.
14.5.3 Centralidad de intermediación (betweenness)
En otra línea, la centralidad de intermediación busca medir una dimensión diferente de la centralidad: cuán importante es el nodo para las conexiones entre el resto de los nodos. Intuitivamente, podríamos considerar que un nodo es más importante si los demás en la red “lo necesitan” para conectarse entre sí (Patty and Penn 2016). En general, interpretamos que los nodos con altos valores de centralidad de entrelazamiento funcionan como puentes de conexión dentro de la red. Para calcular esta medida de centralidad en su versión más básica contaremos los pares de nodos de la red cuyo camino más corto entre ellos (caminos geodésicos) pasa por el nodo en cuestión:
\[\begin{equation} betweenness_i = \sum\limits_{st} \end{equation}\]
donde \(st\) son los pares de nodos en la red; y es igual a 1 si el nodo \(i\) está en el camino geodésico entre \(st\) y 0 si no lo está (o no existe tal camino).
En una red dirigida, sólo se considerarán los enlaces que conducen al nodo específico cuando se calculen sus rutas geodésicas. Si queremos incluir pesos, éstos se interpretarán como distancias que separan los nodos: pesos más altos significarán una conexión más débil. Sin embargo, en múltiples aplicaciones, incluido nuestro ejemplo de copatrocinio, los pesos están destinados a indicar la fuerza de la relación entre dos nodos. En esos casos, podemos invertir los pesos al calcular las distancias geodésicas (¿recuerdas la variable “n_copatrocinio_inv” que creamos anteriormente?), como sugiere M. E. J. Newman (2001).
14.5.4 Cercanía
Por último, la cercanía trata de medir la facilidad de acceso del nodo en cuestión a los demás nodos de la red. En pocas palabras, la idea es que los nodos importantes tendrán conexiones lo suficientemente buenas para acceder fácilmente a cualquier parte de la red. Más formalmente, la proximidad de un nodo es el promedio de las distancias geodésicas (las longitudes de los trayectos geodésicos) que mantiene con todos los demás nodos de la red:
\[closeness_i = \frac{1}{n} \sum{d_{ij}}\]
donde \(i\) es el nodo en cuestión, \(n\) es su número de enlaces, \(j\) es un nodo al que se une, y \(d\) es la distancia geodésica.
Como también se basa en las distancias geodésicas, las mismas consideraciones para las redes ponderadas y dirigidas que revisamos para la interrelación se aplican a la cercanía.
14.6 Aplicación en R
Las medidas de centralidad anteriores tratan de captar las dimensiones de distancia del mismo fenómeno: la importancia de cada nodo de la red. El código para calcularlas usando el tidygraph es relativamente simple. Después de activar el marco de datos de los “nodos,” usaremos mutate() para añadir las estadísticas de centralidad con las múltiples funciones específicas que comienzan con centrality_. Observa que en algunos casos usaremos argumentos para especificar el modo o identificar la variable con pesos en el marco de datos “bordes.” Aquí está la secuencia de tuberías(pipes)59:
tg_copatrocinio_arg_centr <- tg_copatrocinio_arg %>%
activate("nodes") %>% # Las próximas operaciones editarán los "nodos" del tibble
mutate(
# grado
c_in_degree = centrality_degree(mode = "in"),
c_out_degree = centrality_degree(mode = "out"),
# strength (weighted degree)
c_in_strength = centrality_degree(mode = "in", weights = n_copatrocinio),
c_out_strength = centrality_degree(mode = "out", weights = n_copatrocinio),
# weighted pagerank (eigenvector centrality alternative)
c_pagerank = centrality_pagerank(weights = n_copatrocinio),
# betweenness, con o sin pesos invertidos
c_betweenness = centrality_betweenness(),
c_betweenness_w = centrality_betweenness(weights = n_copatrocinio_inv),
# cercanía, con o sin pesos invertidos
c_closeness = centrality_closeness(),
c_closeness_w = centrality_closeness(weights = n_copatrocinio_inv)
)
## Warning: Problem with `mutate()` input `c_closeness`.
## i At centrality.c:2784 :closeness centrality is not well-defined for disconnected graphs
## i Input `c_closeness` is `centrality_closeness()`.
## Warning in closeness(graph = graph, vids = V(graph), mode = mode, weights
## = weights, : At centrality.c:2784 :closeness centrality is not well-
## defined for disconnected graphs
## Warning: Problem with `mutate()` input `c_closeness_w`.
## i At centrality.c:2617 :closeness centrality is not well-defined for disconnected graphs
## i Input `c_closeness_w` is `centrality_closeness(weights = n_copatrocinio_inv)`.
## Warning in closeness(graph = graph, vids = V(graph), mode = mode, weights
## = weights, : At centrality.c:2617 :closeness centrality is not well-
## defined for disconnected graphsPodemos ver que nuestras nueve medidas de centralidad han sido añadidas al marco de datos de los nodos:
tg_copatrocinio_arg_centr
## # A tbl_graph: 46 nodes and 217 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 46 x 13 (active)
## id_sen nombre_sen provincia bloque_politico c_in_degree c_out_degree
## <int> <chr> <chr> <chr> <dbl> <dbl>
## 1 1 RAMON A A~ SANTA CR~ JUSTICIALISTA 8 6
## 2 2 JULIO AMO~ CATAMARCA JUSTICIALISTA 25 4
## 3 3 RAMON A A~ TUCUMAN JUSTICIALISTA 1 4
## 4 4 ALFREDO L~ JUJUY JUSTICIALISTA 1 4
## 5 5 ANTONIO T~ LA PAMPA UCR 14 6
## 6 6 DEOLINDO ~ CHACO JUSTICIALISTA 9 7
## # ... with 40 more rows, and 7 more variables
## #
## # Edge Data: 217 x 5
## from to n_copatrocinio d_copatrocinio n_copatrocinio_inv
## <int> <int> <int> <dbl> <dbl>
## 1 1 2 1 1 1
## 2 1 9 1 1 1
## 3 1 30 1 1 1
## # ... with 214 more rowsComencemos construyendo un simple diagrama de correlación con las medidas de centralidad:
library(ggcorrplot)
corr_centralidad <- tg_copatrocinio_arg_centr %>%
select(starts_with("c_")) %>%
as.data.frame() %>%
# calcular la correlación y redondear a un decimal
cor(use = "pairwise") %>%
round(1)
ggcorrplot(corr_centralidad, type = "lower", lab = T, show.legend = F)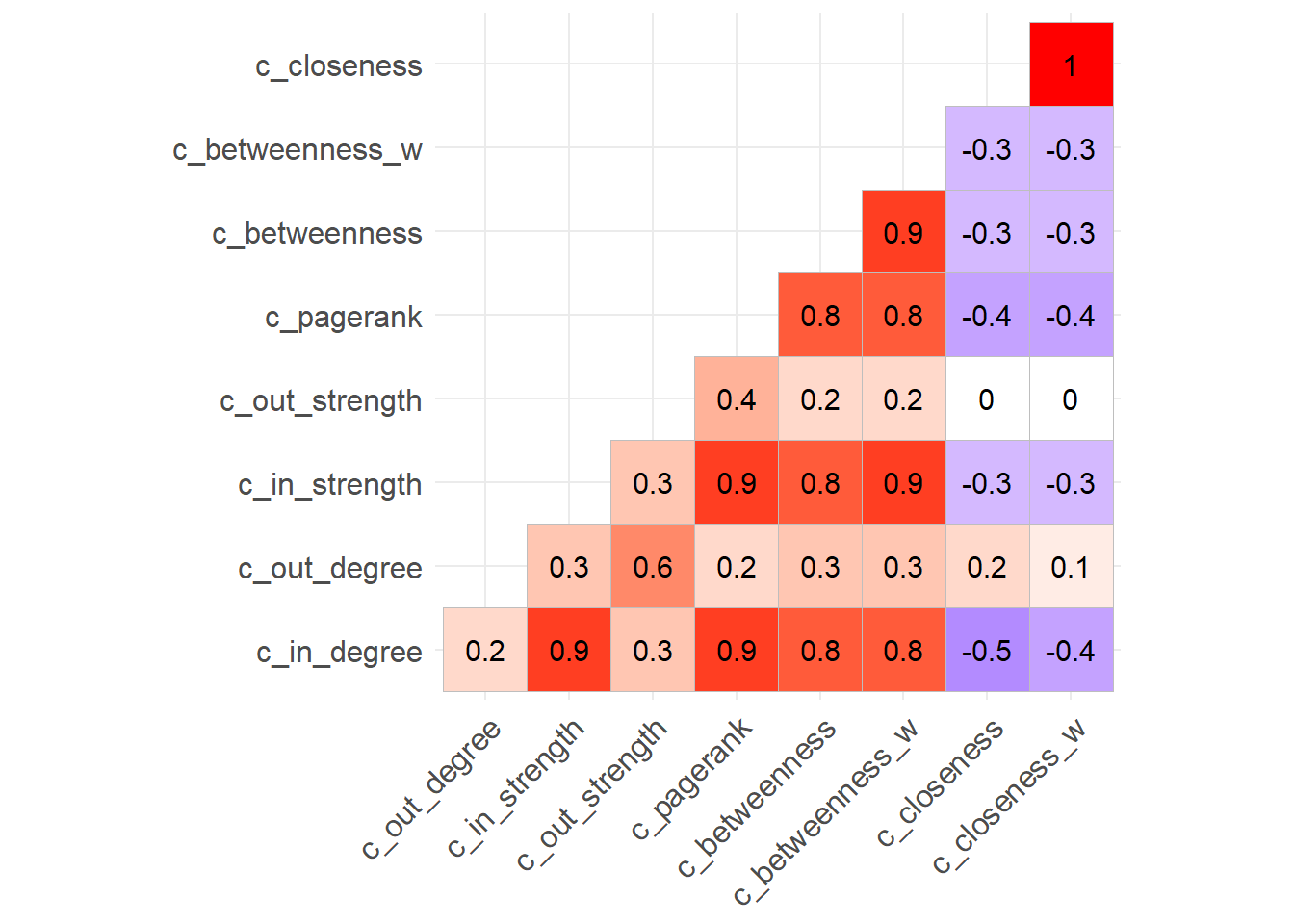
Figura 3.19: Gráfico de correlación entre distintas medidas de centralidad
Observa que las correlaciones más fuertes en la trama existen entre las medidas de grado, intensidad y PageRank, lo que generalmente se espera. Notablemente, in-degree no exhibe esa fuerte correlación con out-degree (lo mismo ocurre con in-strength y out-strength), lo que sugiere que el grupo de legisladores bien patrocinados no es el mismo que el grupo de legisladores que generalmente actúan como patrocinadores.
Podemos obtener fácilmente los legisladores con el mayor in-degree y out-degree de nuestro objeto tg_copatrocinio_arg_centrality:
tg_copatrocinio_arg_centr %>%
arrange(-c_in_degree) %>%
select(id_sen, nombre_sen, c_in_degree)
## # A tbl_graph: 46 nodes and 217 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 46 x 3 (active)
## id_sen nombre_sen c_in_degree
## <int> <chr> <dbl>
## 1 2 JULIO AMOEDO 25
## 2 43 HECTOR J VELAZQUEZ 22
## 3 34 OLIJELA DEL VALLE RIVAS 20
## 4 9 ORALDO N BRITOS 19
## 5 31 ANTONIO O NAPOLI 17
## 6 5 ANTONIO TOMAS BERHONGARAY 14
## # ... with 40 more rows
## #
## # Edge Data: 217 x 5
## from to n_copatrocinio d_copatrocinio n_copatrocinio_inv
## <int> <int> <int> <dbl> <dbl>
## 1 9 1 1 1 1
## 2 9 4 1 1 1
## 3 9 8 1 1 1
## # ... with 214 more rowstg_copatrocinio_arg_centr %>%
arrange(-c_out_degree) %>%
select(id_sen, nombre_sen, c_out_degree)
## # A tbl_graph: 46 nodes and 217 edges
## #
## # A directed simple graph with 1 component
## #
## # Node Data: 46 x 3 (active)
## id_sen nombre_sen c_out_degree
## <int> <chr> <dbl>
## 1 12 PEDRO A CONCHEZ 8
## 2 31 ANTONIO O NAPOLI 8
## 3 6 DEOLINDO FELIPE BITTEL 7
## 4 10 JORGE A CASTRO 7
## 5 23 MARGARITA MALHARRO DE TORRES 7
## 6 28 FAUSTINO M MAZZUCCO 7
## # ... with 40 more rows
## #
## # Edge Data: 217 x 5
## from to n_copatrocinio d_copatrocinio n_copatrocinio_inv
## <int> <int> <int> <dbl> <dbl>
## 1 8 28 1 1 1
## 2 8 34 1 1 1
## 3 8 24 1 1 1
## # ... with 214 more rowsLa escala de esas dos medidas es notable. El senador de mayor rango, Julio Amoedo, recibió el patrocinio de 25 legisladores diferentes (¡más de la mitad del Senado!). En cambio, el senador de mayor grado de salida, Pedro Conchez, patrocinó los proyectos de ley de sólo 8 legisladores distintos. Esto podría indicar que, si bien el papel de un “patrocinador principal” está bien definido, el de un “apoyador” no lo está.
Otra forma común de utilizar los puntajes de centralidad implica analizarlos de acuerdo a algunas de las otras variables relevantes en nuestros datos. Esto se facilita con la estructura de objetos del tidygraph, que integra en un marco de datos toda la información de los nodos (incluyendo las variables descriptivas y los puntajes de centralidad). Por ejemplo, podemos trazar la relación entre PageRank/in-degree/in-strengh y los dos principales bloques políticos con un simple gráfico de cajas:
ggplot(data = tg_copatrocinio_arg_centr %>%
as_tibble() %>%
filter(bloque_politico %in% c("UCR", "JUSTICIALISTA")),
aes(x = bloque_politico, y = c_pagerank)) +
geom_boxplot()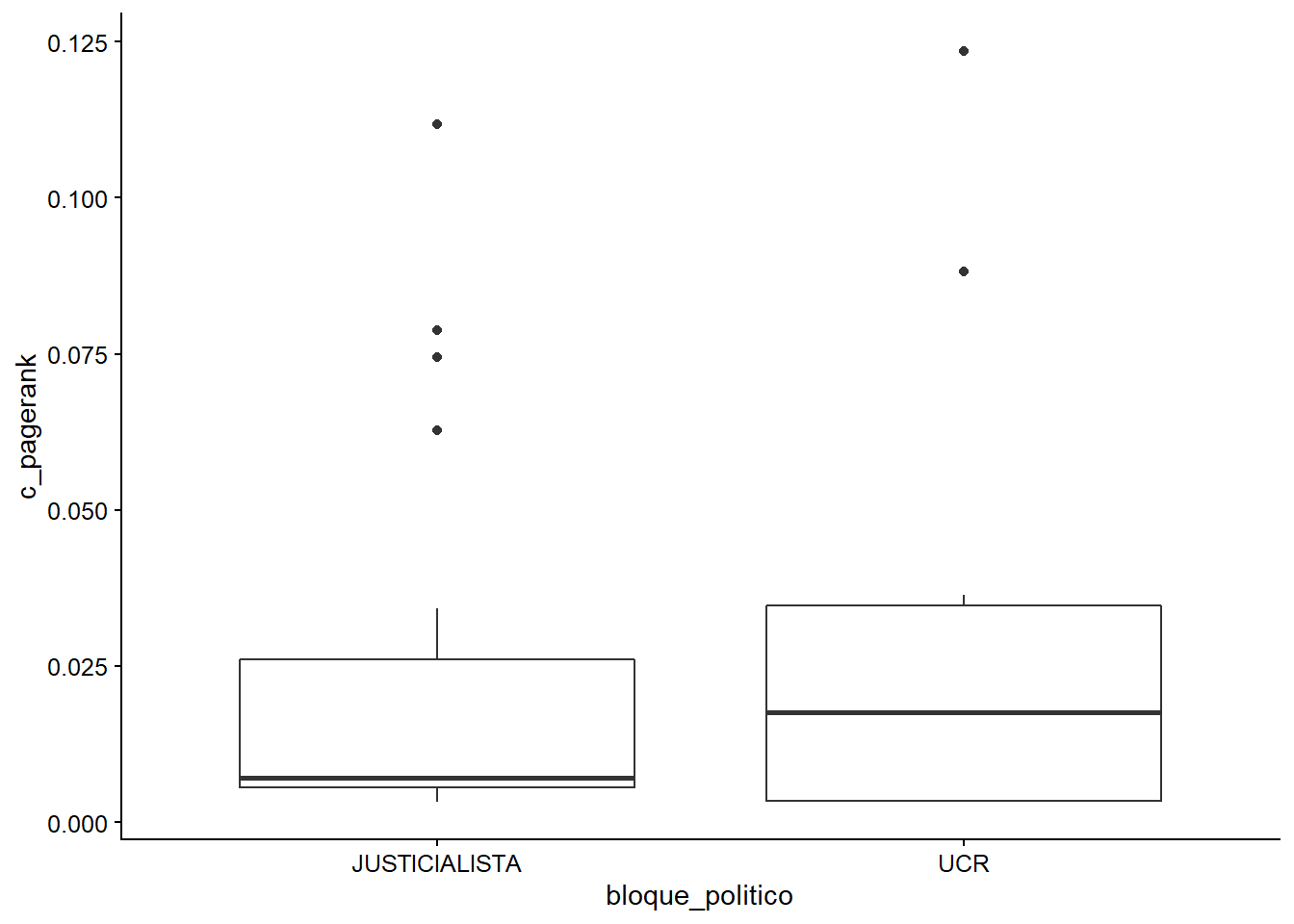
Figura 3.22: PageRank por bloque político
Si bien el rango de las medidas del PageRank es comparable, la forma de los gráficos de cajas sugiere que los dos bloques políticos se comportan de manera diferente cuando se trata de copatrocinio. Mientras que el bloque justicialista tiene unos pocos legisladores notables, que presumiblemente actúan como patrocinadores principales bien respaldados, el resto de sus senadores no son tan influyentes en ese sentido. Por otra parte, aunque la UCR también tiene un par de legisladores notables, la distribución parece ser más equilibrada.
Ejercicio 14C. Crea un gráfico para comparar algún puntaje de centralidad por si el legislador es del área metropolitana (como en el ejercicio anterior).
A lo largo de este capítulo, cubrimos las nociones básicas del análisis de redes en las ciencias sociales. Te recomendamos leer la bibliografía recomendada al principio del capítulo para poder expandir tu análisis aún más.
Correo electrónico: arcruz@uc.cl↩︎
Esta tercera red, como se describe en nuestro ejemplo, no registra cuando dos legisladores apoyan conjuntamente un proyecto de ley de un legislador diferente. Sólo mide el apoyo directo entre pares de legisladores↩︎
R devuelve una advertencia para las funciones de cercanía, porque el algoritmo tiene problemas cuando se trata de redes desconectadas. Para obtener la cercanía de un nodo en particular, es necesario conocer su distancia geodésica a cada uno de los otros nodos de la red. Lo que hay que hacer cuando algunas rutas geodésicas no existen no es sencillo, lo que hace que el cálculo y la interpretación sean complicados (ver Opsahl, Agneessens, and Skvoretz 2010)↩︎