Capítulo 16 Mapas y datos espaciales
Andrea Escobar62 y Gabriel Ortiz63
Lecturas sugeridas
Brunsdon, C. and Comber, L. (2015). An Introduction to R for Spatial Analysis and Mapping. SAGE, Thousand Oaks, CA.
Lansley, G. and Cheshire, J. (2016). An Introduction to Spatial Data Analysis and Visualisation in R. Consumer Data Research Centre.
Lovelace, R., Nowosad, J., and Münchow, J. (2019). Geocomputation with R. CRC Press, Boca Raton, FL.
Pebesma, E. (2018). Simple Features for R: Standardized Support for Spatial Vector Data. The R Journal, 10(1):439–446.
Los paquetes que necesitas instalar
tidyverse(Wickham 2019b),paqueteadp(Urdinez and Cruz 2020),sf(Pebesma 2020),ggrepel(Slowikowski 2020),gridExtra(Auguie 2017),rnaturalearthhires(South 2020),spdep(R. Bivand 2019).
16.1 Introducción
En este capítulo, aprenderemos a trabajar con datos espaciales usando R y tidyverse. Nos centraremos en la riqueza que tienen los datos espaciales, tanto como herramienta para el análisis de datos exploratorios sobre diversos fenómenos, como para visualizar y comunicar nuestros hallazgos de una forma atractiva y efectiva. Como tal, este capítulo tiene los siguientes objetivos:
Describir el formato de los datos espaciales.
Explicar por qué estos datos son interesantes para ser utilizados en el análisis de las ciencias políticas.
Su manejo y manipulación en R, centrándose en su visualización mediante la creación de mapas estáticos y dinámicos con
ggplot2.No entraremos en la elaboración de modelos estadísticos inferenciales a partir de datos espaciales (Modelos con lag espacial), ni tampoco en la generación de datos geográficos, ya que trabajaremos sobre conjuntos de datos geográficos ya creados.
El conjunto de datos que utilizaremos en este capítulo será un shapefile (formato que explicaremos más adelante) de los estados de Brasil, obtenido del Spatial Data Repository of New York University, que se fusionará con los datos de Freire (2018).
Por un lado, el depósito de datos espaciales de la Universidad de Nueva York proporciona muchos datos espaciales de diferentes países, así como de divisiones supranacionales y subnacionales. En este caso, utilizaremos una base de datos de las fronteras estatales de Brasil en el año 1991, proporcionadas por el Instituto Brasileño de Geografía y Estadística. Por otro lado, el trabajo de Freire (2018) explica la causa de la disminución de la tasa de homicidios en el estado de Sao Paulo como resultado de la implementación de políticas estatales para la reducción del crimen. Este trabajo es útil ya que recoge datos a nivel estatal de diferentes indicadores socioeconómicos como el PIB, el Índice de Gini, el promedio de años de escolaridad, entre otros, en un período de veinte años (1990-2010). Estos datos se unirán a nuestro shapefile para trazar estas variables en mapas.
También presentamos una serie de ejercicios que te ayudarán a ganar experiencia utilizando un shapefile de América del Sur fusionado con datos del PIB per cápita y la calidad de la democracia electoral de cada país tomados de la base de datos de V-Dem.
16.1.1 Datos espaciales: ¿qué son?
Los datos espaciales, o más bien los datos geoespaciales, se refieren a los datos obtenidos de lugares geográficos, es decir, de zonas de la superficie de la Tierra. El uso de este tipo de datos reconoce “la importancia de conceptos espaciales como distancia, ubicación, proximidad, vecindad y región en la sociedad humana,” permitiéndonos enfrentar los fenómenos desde una perspectiva multivariante y multidimensional, proporcionándonos información adicional para nuestras observaciones (CSISS 2004).
En ciencia política, la perspectiva espacial para el análisis de datos ha avanzado gracias a trabajos como el de Gary King (1997) sobre cómo hacer inferencias ecológicas, y el de Gimpel y Schuknecht (2003) sobre la accesibilidad a los lugares de votación. Este tipo de datos permite responder a preguntas como la influencia de la proximidad de los países vecinos en la difusión de ciertas políticas, pero también resulta ser una herramienta clave en la exploración de datos para observar la existencia de patrones territoriales en otros estudios.
En los últimos años, los datos espaciales se han difundido ampliamente, sobre todo gracias a las iniciativas de los gobiernos que proporcionan datos para diversos procesos sociales y económicos del país. Las nuevas plataformas de acceso abierto, como Google Maps o Open Street Map, y las redes sociales como Twitter y Facebook también contribuyeron al interés por los datos espaciales. Mientras tanto, para los investigadores y estudiantes, las bases datos como la ya mencionada del Depósito de Datos Espaciales de la Universidad de Nueva York proporcionan archivos shapefile de fácil acceso y manipulación para generar visualizaciones y unir datos georreferenciados de otras bases de datos.
16.1.2 Estructura de datos espaciales
Los archivos que contienen datos espaciales se conocen comúnmente como shapefiles, que generalmente se colocan en una carpeta que contiene al menos tres archivos con las extensiones .shp, .dbf y .shx.
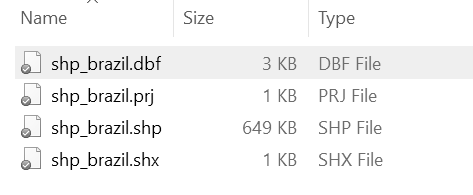
Figura 16.1: Ejemplo de una carpeta que contiene un shapefile en Windows. Ten en cuenta que el archivo .shp contiene la gran mayoría de la información. Además, esta carpeta contiene un archivo .prj adicional
En R, los shapefiles se suelen representar mediante vectores, que consisten en la descripción de la geometría o forma (shape) de los objetos. Generalmente contienen variables adicionales, llamadas atributos, sobre los mismos datos. Usando como ejemplo los datos que serán analizados a lo largo de este capítulo, nuestra base de datos describe las fronteras de los estados de Brasil (geometría), y también contiene información de la tasa de homicidios más otros datos socioeconómicos (atributos). Los datos espaciales son diversos en sus características y generalmente se dividen en tipos de vectores que en cada caso consisten en un conjunto de pares de coordenadas (x,y):
Puntos: Una sola ubicación descrita por un punto como la dirección de una casa geocodificada.
Líneas: Un segmento compuesto por una serie de puntos conectados entre sí que no forman un objeto cerrado.
Polígonos: Una superficie plana compuesta por una serie de líneas conectadas entre sí que forman un objeto cerrado.
Multi-polígonos: Multi-superficies compuestas de polígonos que no necesariamente se intersectan.
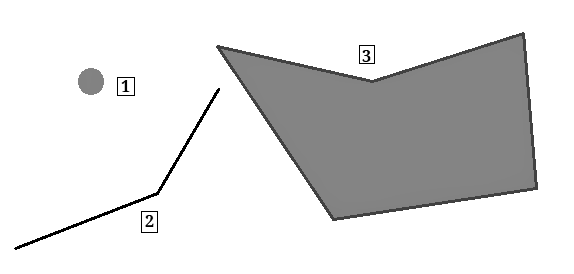
Figura 16.2: Tipos de formas en los datos espaciales. (1) Punto, (2) Línea, (3) Polígono
Tip. Como hemos dicho, el Repositorio de Datos Espaciales de la Universidad de Nueva York puede ser una buena alternativa si quieres empezar a trabajar con datos espaciales de tu país, estado o municipio. Puede buscar fácilmente archivos de forma entrando en la página web del Repositorio y seleccionando “Polígono” en la categoría “Tipo de datos.” Después de eso, tienes que introducir el nombre del área de interés en el buscador, seleccionar un resultado y presionar “Descargar Shapefile” en la esquina superior derecha de la página. Otra ventaja de estos datos es que los archivos suelen ser livianos, pero de suficiente calidad, lo que resulta conveniente en el caso de los equipos con limitaciones para procesar archivos de datos de gran tamaño.
16.2 Datos espaciales en R
En los últimos años, R ha mejorado considerablemente sus herramientas para manipular y analizar datos geográficos de manera que sean compatibles con la sintaxis y las funcionalidades de otros paquetes del programa. En el pasado, estas tareas eran demasiado desafiantes. En este capítulo, nos centraremos en el paquete sf, que fue creado en 2016 sobre las funcionalidades base de tres paquetes anteriores: sp, rgeo y rgdal, y que implementa el modelo estándar de código abierto características simples64. sf permite la representación de objetos del mundo real en el ordenador, que poseen atributos tanto espaciales como no espaciales, basados en la geometría 2D con interpolación lineal entre vértices (Pebesma 2018).
16.2.1 Características simples en R
La principal ventaja que proporciona el paquete sf es que nos permite trabajar con datos espaciales dentro del tidyverse, es decir, podemos manejar los datos espaciales como si fueran cualquier otro tipo de base de datos. Podemos hacerlo mediante funciones de R contenidas en el metapaquete tidyverse, como ggplot2 y dplyr, en línea con lo que hemos aprendido a lo largo del libro^[Algunas opciones alternativas para construir mapas en R son los paquetes tmap y cartogram, que se explican en profundidad en el Capítulo 8 de “Geocomputación con R” de65.
Es importante tener la última versión de tidyverse para ejecutar las utilidades de ggplot2 que se usarán en este capítulo. Puedes actualizarlo a la última versión con el comando install.packages("tidyverse"):
library(tidyverse)Ahora tenemos que instalar el paquete sf. Para que esto funcione en Mac y Linux necesitas las últimas versiones de FDAL, GEOS, Proj.4 y UNDUNITS ya instaladas66. Una vez hecho esto podemos instalar el paquete sf:
devtools::install_github("robinlovelace/geocompr")
install.packages("sf")
library(sf)16.2.2 Estructura
Para ver la estructura de los objetos de tipo sf cargamos nuestra base de datos en el formato shapefile, usando la función read_sf() (nota que estamos cargando el archivo shp_brasil.shp contenido en la carpeta shp_brasil):
shp_brasil <- read_sf("datos_espaciales/shp_brasil.shp")En la siguiente imagen, detallamos las partes de nuestro shapefile con sus nombres:
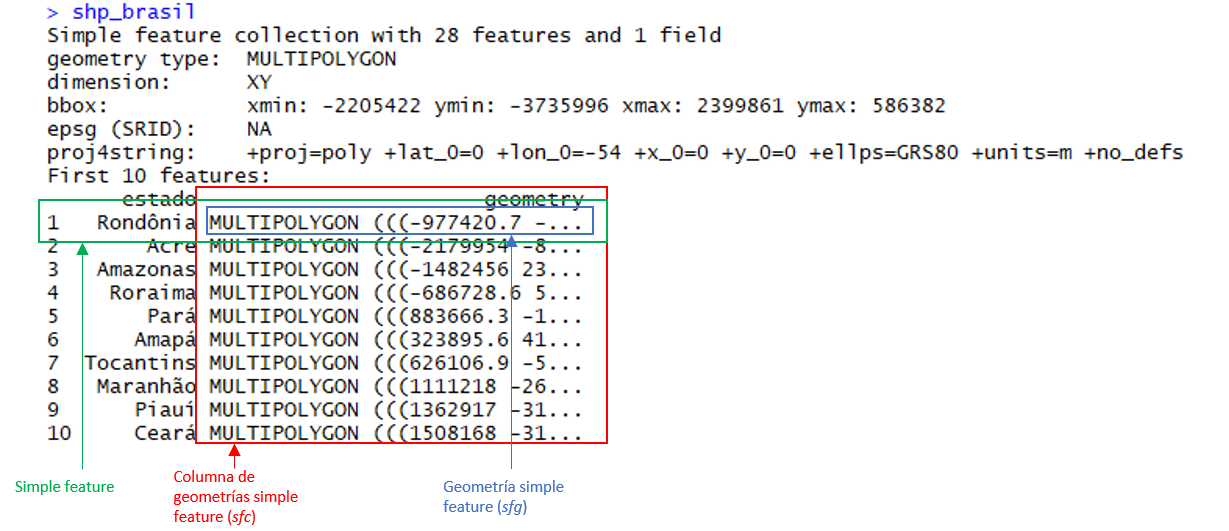
Figura 16.3: Estructura de un objeto sf
Como se puede observar en la figura anterior, las características simples se guardan por sf en un formato data.frame y con un formato adicional de clase sf. Entonces, como se ha dicho antes, podemos dirigir este conjunto de datos como cualquier otro dentro del tidyverse, usando sus funciones, pipas (pipes o %>%), etc. Aquí, cada fila consiste en una simple característica, y cada columna consiste en un atributo. La diferencia con una base de datos normal es que aquí encontramos una nueva columna de geometrías de rasgos simples (single-featured geometry column - sfc), lo que resulta en un marco de datos con una columna extra para información espacial.
Podemos verificar esto comprobando el tipo de archivo que hemos cargado con la función class(). Observe que shp.brasil es, al mismo tiempo, un archivo de tipo sf y un data.frame:
class(shp_brasil)
## [1] "sf" "tbl_df" "tbl" "data.frame"Ahora, si exploramos nuestros datos con mayor detalle encontraremos que este estándar puede ser implementado en diferentes tipos de geometría en nuestra base de datos:
- Un vector numérico para un solo punto (POINT)
- Una matriz numérica (cada fila es un punto) para una serie de puntos (MULTIPOINT o LINE)
- Una lista de matrices para un grupo de conjuntos de puntos (MULTILINESTRING, POLYGON)
- Una lista de matrices (MULTIPOLYGON) que se convierte en la más utilizada cuando los datos geográficos se representan como forma y ubicación de los países u otras unidades administrativas de éstos.
- Una lista de cualquiera de los elementos anteriormente mencionados (GEOMETRYCOLLECTION)
Usando la función st_geometry() podemos ver la geometría incluida en nuestro shapefile:
st_geometry(shp_brasil)
## Geometry set for 28 features
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -2200000 ymin: -3700000 xmax: 2400000 ymax: 590000
## projected CRS: Polyconic
## First 5 geometries:Una vez cargado nuestro shapefile, podemos empezar a generar mapas. Ten en cuenta que la forma de hacerlo se basa en ggplot2; sólo tenemos que seleccionar nuestra base de datos y añadir el geom geom_sf()67.
ggplot(data = shp_brasil) +
geom_sf()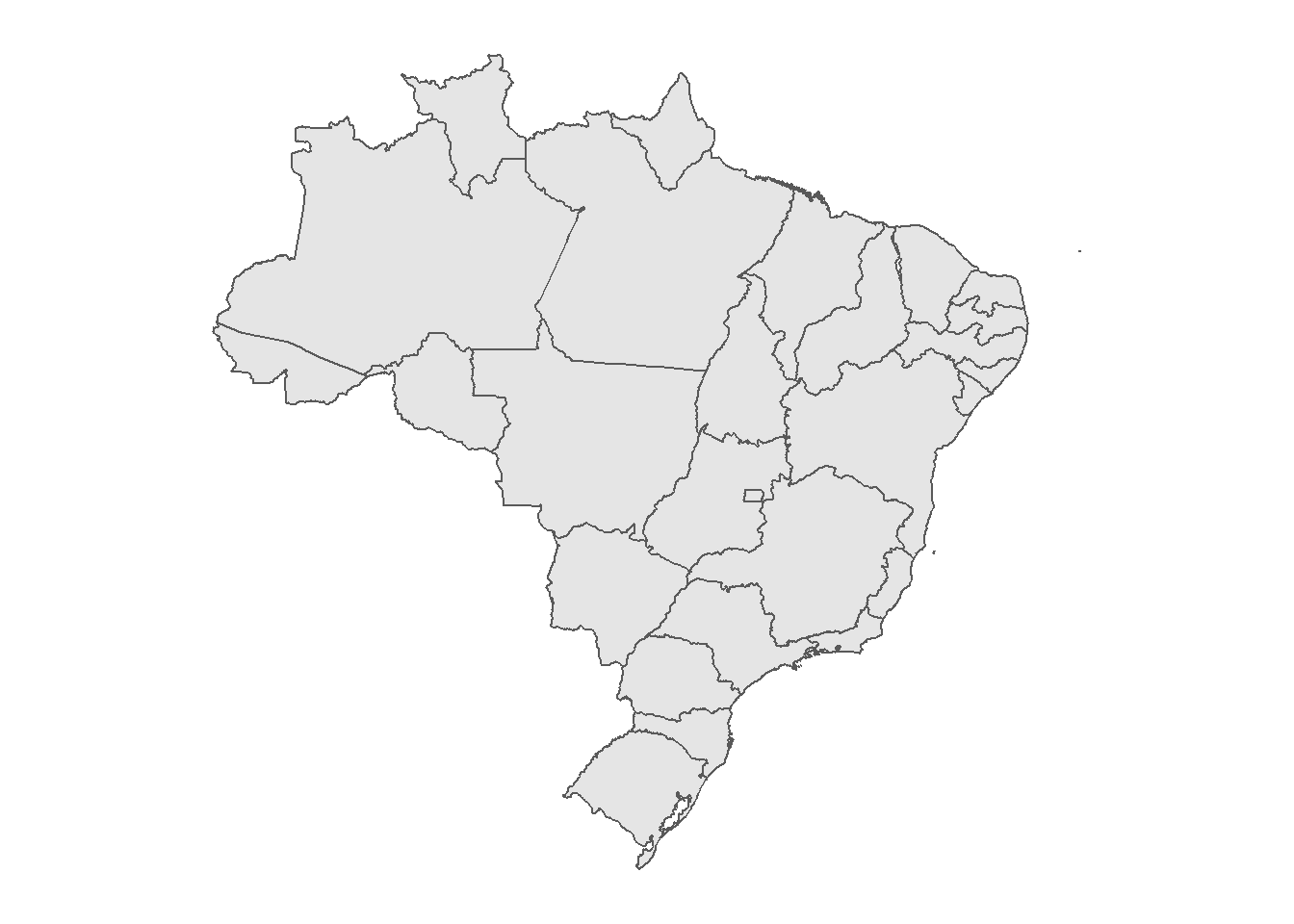
Figura 3.8: Mapa de los estados de Brasil
Ejercicio 16A. 1. Descarga el shapefile de Sudamérica de ArcGIS y cárgalo en R usando
read_sf(). Selecciona sólo las variables “CNTRY_NAME,” “ISO_3DIGIT” y “geometry.” 2. Filtra la base de datos por la variable ‘CNTRY_NAME’ para eliminar las observaciones de “South Georgia & the South Sandwich Is.” y “Falkland Is.” 3. Trazar el shapefile usandoggplot()ygeom_sf().
16.3 Gestión de Datos Espaciales
Ya aprendimos a cargar archivos de forma con read_sf(). Ahora que hemos cargado el archivo, procederemos a aprender qué tipo de modificaciones podemos hacer para generar nuevos datos a partir de la información que ya tenemos. También mostraremos cómo unir datos de otras bases de datos a nuestro shapefile.
16.3.1 Modificaciones
Hay dos maneras de hacer modificaciones en nuestra base de datos georeferenciada. La primera consiste en aplicar las técnicas que ya hemos aprendido usando el tidyverse, mientras que la segunda consiste en usar las funciones incorporadas en el paquete sf. En este paquete, todas las funciones empiezan con st_, para que puedan ser fácilmente comprendidas en la herramienta de completado de RStudio. Estas funciones se utilizan principalmente para transformar y realizar operaciones geográficas. En estas secciones combinaremos ambas técnicas para generar nuevas variables y datos asociados a nuestra base de datos.
16.3.1.1 Filtrar y seleccionar por unidades geográficas
Una de las primeras funciones que podemos utilizar las funciones de dplyr para seleccionar datos dentro de nuestra base. Así, por ejemplo, podemos ocupar filter() para seleccionar ciertos estados de Brasil, como por ejemplo el estado de São Paulo:
shp_brasil %>%
filter(estado == "São Paulo")
## Simple feature collection with 1 feature and 1 field
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: 92000 ymin: -2800000 xmax: 1e+06 ymax: -2200000
## projected CRS: Polyconic
## # A tibble: 1 x 2
## estado geometry
## * <chr> <MULTIPOLYGON [m]>
## 1 São Paulo (((719692 -2716734, 719500 -2717678, 719210 -2716889, 719362~Un desafío común que a menudo enfrentamos cuando trabajamos con shapefiles de países enteros es la existencia de regiones o zonas insulares que forman parte del territorio administrativo pero que están aisladas geográficamente, por ejemplo, la Isla de Pascua en Chile o las Islas Galápagos en Ecuador. Por diversas razones, el acceso a los datos de esas regiones es limitado y a menudo se dejan fuera del análisis. Por lo tanto, estamos interesados en sacar estas regiones de nuestro shapefile. En Brasil, el Distrito Estatal de Fernando de Noronha, un archipiélago de 21 islas situado en el Océano Atlántico es uno de este tipo de casos (es posible identificarlo como un pequeño punto en la parte superior derecha del mapa anterior). Podemos eliminar fácilmente este tipo de datos de nuestro shapefile, de nuevo, con la función filter().
shp_brasil <- shp_brasil %>%
filter(estado != "State District of Fernando de Noronha (PE)")Esto se reflejará en los siguientes mapas:
ggplot(data = shp_brasil) +
geom_sf()
Figura 3.11: Mapa de los estados brasileños excepto el Distrito Estatal de Fernando de Noronha
16.3.1.2 Generar nuevas unidades con st_union()
Otra opción interesante es generar nuevas variables que agrupen múltiples unidades geográficas. Al hacer esto, estaremos generando efectivamente nuevas unidades geográficas más allá de la información inicial contenida en nuestro shapefile. Por ejemplo, en 1969 el Instituto Brasileño de Geografía y Estadística dividió el país en 5 regiones que agrupan los 27 estados del país. Dado que se trata de una división con fines académicos, y no reconocida en términos político-administrativos, no es posible encontrar archivos de tipo shapefile que muestren estas regiones. Sin embargo, usando mutate() y case_when(), podemos generar fácilmente esta categoría nosotros mismos:
shp_brasil <- shp_brasil %>%
mutate(region = case_when(
estado %in% c("Goiás", "Mato Grosso", "Mato Grosso do Sul",
"Distrito Federal") ~ "Centro-Oeste",
estado %in% c("Acre", "Amapá", "Amazonas", "Pará", "Rondônia", "Roraima",
"Tocantins") ~ "Norte",
estado %in% c("Alagoas", "Bahia", "Ceará", "Maranhão", "Paraíba",
"Pernambuco", "Piauí", "Rio Grande do Norte",
"Sergipe") ~ "Noroeste",
estado %in% c("Espírito Santo", "Minas Gerais", "Rio de Janeiro",
"São Paulo") ~ "Sudeste",
estado %in% c("Paraná", "Rio Grande do Sul",
"Santa Catarina") ~ "Sur")
)Una vez generada, podemos incorporar esta variable a nuestro mapa:
ggplot(data = shp_brasil)+
geom_sf(aes(fill = region))+
labs(fill = "Región")
Figura 3.13: Mapa de los estados brasileños agrupados por región
Mejor aún, podemos usar esta categoría para generar nueva geometría con group_by(), summarize() y st_union():
shp_brasil_regions <- shp_brasil %>%
group_by(region) %>%
summarize(geometry = st_union(geometry)) %>%
ungroup()Podemos graficar este resultado con ggplot():
ggplot(shp_brasil_regions) +
geom_sf(aes(fill = region))+
labs(fill = "Región")
Figura 3.15: Mapa de las regiones del Brasil
Observa que esto no genera objetos completamente “planos,” es decir, todavía podemos observar algunas líneas dentro de ellos, probablemente porque los polígonos de nuestro shapefile no se superponen perfectamente. Esta es una dificultad común cuando se realizan este tipo de operaciones, e incluso puede ocurrir cuando se trabaja con shapefiles sofisticados. A pesar de las dificultades, estas operaciones son beneficiosas cuando, por ejemplo, se elaboran distritos electorales compuestos por varias provincias o municipios.
16.3.1.3 Crear nuevos shapefiles con st_write()
Podemos guardar este nuevo shapefile con las funciones st_write(), en las que sólo tenemos que seleccionar el objeto que queremos guardar y la ruta donde queremos que se guarde. En este caso, guardaremos el archivo shp_brasil_regions.shp en una carpeta con el mismo nombre. Esto generará automáticamente no sólo el .shp, sino también todos los demás archivos que constituyen el shapefile:
dir.create("shp_brasil_regions/")
st_write(shp_brasil_regions, "shp_brasil_regions/shp_brasil_regions.shp")Advertencia: El comando
st_write()no puede sobreescribir los archivos existentes y al intentarlo se informará automáticamente de un error. Si quieres modificar un shapefile ya generado, tienes que borrarlo manualmente de su carpeta antes de generar los nuevos archivos.
16.3.2 Añade datos de otras bases de datos con left_join()
En primer lugar, aprenderemos a añadir datos de otras bases de datos a nuestro shapefile, ya que normalmente querremos conocer los atributos de nuestras ubicaciones geográficas para generar un análisis de inferencia exploratorio o estadístico. Para ejemplificarlo, cargaremos la base de datos de Freire (previamente eliminamos algunos datos para simplificar las base de datos):
library(paqueteadp)
data("estados_brasil")Nota que nuestra base de datos contiene la variable estado. Esta misma variable se encuentra en nuestro shapefile:
head(estados_brasil$estado)
## [1] "Acre" "Acre" "Acre" "Acre" "Acre" "Acre"
head(shp_brasil$estado)
## [1] "Rondônia" "Acre" "Amazonas" "Roraima" "Pará" "Amapá"Nos hemos asegurado previamente de que las observaciones estén codificadas de la misma manera tanto en la base de datos como en el shapefile.68 Haciendo esto, podemos unir ambas bases de datos con el comando left_join():
shp_brasil_data <- shp_brasil %>%
left_join(estados_brasil)Usando head() podemos ver el resultado de esta operación:
head(shp_brasil_data)
## Simple feature collection with 6 features and 7 fields
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -1400000 ymin: -1500000 xmax: -630000 ymax: -890000
## projected CRS: Polyconic
## # A tibble: 6 x 8
## estado geometry region estado_cod anio
## <chr> <MULTIPOLYGON [m]> <chr> <dbl> <dbl>
## 1 Rondô~ (((-977421 -892385, -975~ Norte 11 1990
## 2 Rondô~ (((-977421 -892385, -975~ Norte 11 1991
## 3 Rondô~ (((-977421 -892385, -975~ Norte 11 1992
## # ... with 3 more rows, and 3 more variablesUna vez que la información de Freire se incorpore a nuestro shapefile, estos datos serán útiles cuando empecemos a mapear las variables.
Ejercicio 16B. 1. Selecciona los países del Cono Sur (Chile, Argentina y Uruguay) y grafícalos. 2. Genera un nuevo shapefile con las subregiones de América del Sur. Sugerimos lo siguiente: + Mar Caribe, correspondiente a Colombia, Venezuela, Surinam, Guayana y Guayana Francesa. + Región Andina, correspondiente a Bolivia, Ecuador, Perú y Colombia. + Región Oriental, correspondiente a Brasil y a Paraguay. + Cono Sur, correspondiente a Chile, Argentina y Uruguay. 3. Descarga la base de datos ampliada (‘Country-Year: V-Dem Full+Others’) de V-Dem y selecciona sólo las siguientes variables: ‘country_name,’ ‘country_text_id,’ ‘year,’ ‘v2x_polyarchy,’’ e_migdppc’. Fíltralas para considerar sólo el período entre 1996 y 2016 (los últimos 20 años, para los que hay datos disponibles para todas las variables). 4. Usando
left_join(), añade el shapefile original a la base de datos cargada del ejercicio anterior. Consejo: utiliza los argumentosby.x="ISO_3DIGIT"yby.y="country_text_id""). Revisa la base de datos. Notarás que falta un país. ¿Cuál es?
16.4 Mapeo
Los mapas han sido históricamente la principal técnica para almacenar y comunicar datos espaciales, y los objetos y sus atributos pueden ser fácilmente moldeados de manera que el ojo humano pueda reconocer rápidamente patrones y anomalías en un mapa bien diseñado. (ver Spatial Analysis Online). En esta sección, aprenderás a hacer diferentes tipos de mapas (tanto estáticos como animados) a partir de datos geográficos y sus atributos, utilizando el formato ggplot2 como base.
16.4.1 Generando centroides
La primera opción es generar nuevas variables asociadas a nuestras unidades usando el comando mutate. Una acción común es generar lo que se llama “centroides,” es decir, puntos situados en el centro de nuestras unidades. Para generar los centroides, necesitamos crear las siguientes variables asociadas a nuestros geoms: centroid, coords, coords_x y coords_y. Podemos hacer esto con los comandos map() y map_dbl(), del paquete purr, y los comandos st_centroid() y st_coordinates(), del paquete sf.
shp_brasil <- shp_brasil %>% mutate(centroid = map(geometry, st_centroid),
coords = map(centroid, st_coordinates), coords_x = map_dbl(coords, 1),
coords_y = map_dbl(coords, 2))
head(shp_brasil)
## Simple feature collection with 6 features and 6 fields
## geometry type: MULTIPOLYGON
## dimension: XY
## bbox: xmin: -2200000 ymin: -1500000 xmax: 880000 ymax: 590000
## projected CRS: Polyconic
## # A tibble: 6 x 7
## estado geometry region centroid coords coords_x
## <chr> <MULTIPOLYGON [m]> <chr> <list> <list> <dbl>
## 1 Rondô~ (((-977421 -892385, -975~ Norte <XY [2]> <dbl[~ -9.68e5
## 2 Acre (((-2179954 -836549, -20~ Norte <XY [2]> <dbl[~ -1.81e6
## 3 Amazo~ (((-1482456 230568, -147~ Norte <XY [2]> <dbl[~ -1.19e6
## # ... with 3 more rows, and 1 more variableUna vez generadas, podemos graficar estas variables con ggplot() y el paquete ggrepel para generar el texto:
library(ggrepel)ggplot(data = shp_brasil) +
geom_sf()+
geom_text_repel(mapping = aes(coords_x, coords_y, label = estado),
size = 4, min.segment.length = 0)+
labs(x = "", y = "")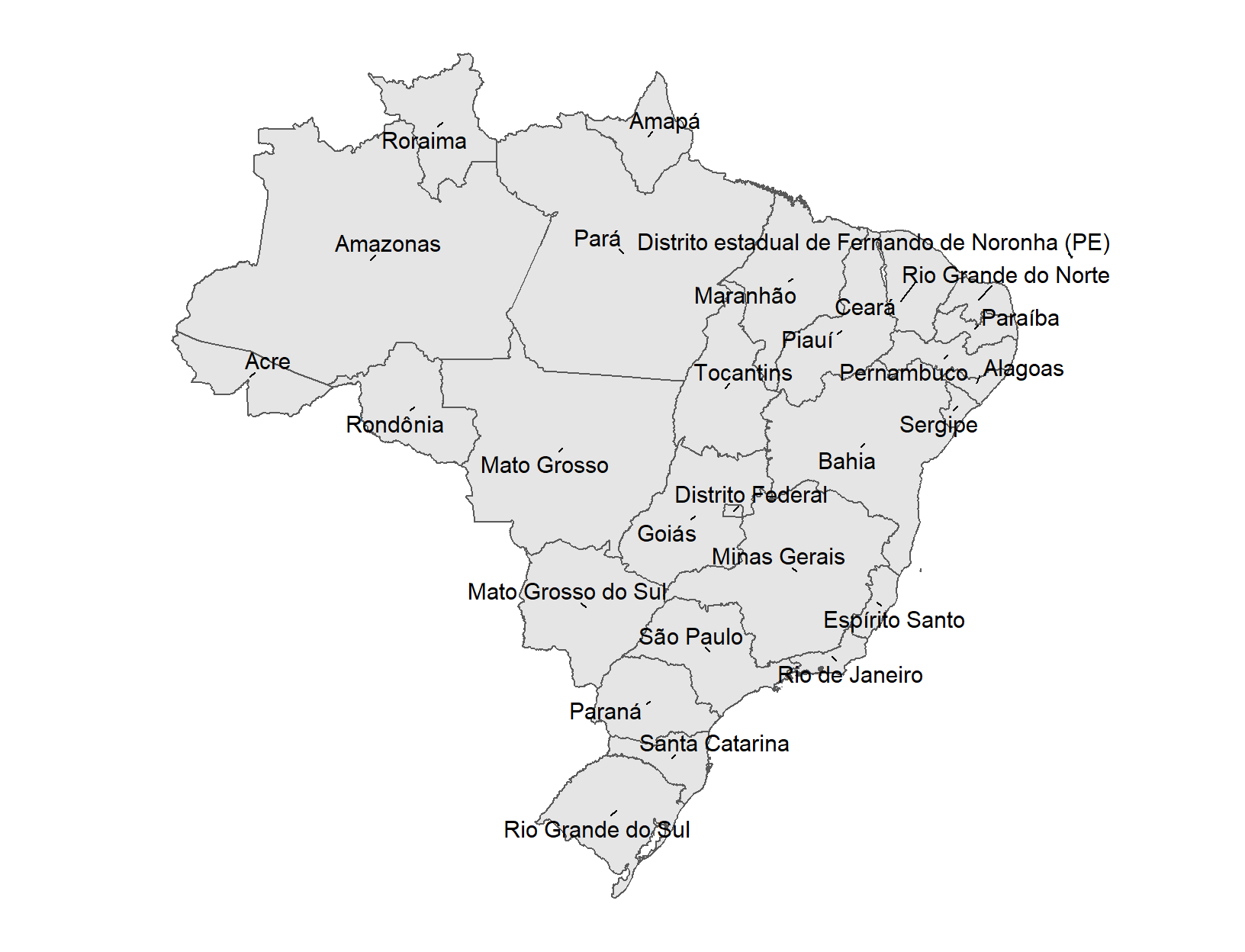
Figura 3.22: Mapa de Brasil con los nombres de sus estados
16.4.2 Mapeando variables
Podemos generar visualizaciones más complejas de elementos que ya hemos visto en secciones anteriores. Por ejemplo, podemos mapear una variable continua de acuerdo a un color, usando el mapeo estético fill = de ggplot2:
ggplot(data = shp_brasil_data) +
geom_sf(aes(fill = gini)) +
labs(fill = "Índice Gini")
Figura 3.23: Mapa de Brasil sin coordenadas y líneas cartesianas
16.4.3 Mapeando puntos
Si, aparte de los polígonos, tenemos datos que denotan las ubicaciones de los eventos que han ocurrido dentro del espacio que cubre todo nuestro shapefile, también es posible graficar toda esa información en un grupo. En este caso, aprenderemos dos maneras de realizar esta tarea; una usando geom_sf, y la otra, usando un geom que ya hemos visto anteriormente en el libro: geom_point().
Para este ejemplo, utilizaremos un ejemplo adaptado de Freire et al. (2019) que corresponde a un estudio que georeferencia las víctimas mortales del periodo dictatorial de Augusto Pinochet entre 1973 y 1990. Este paquete, bajo el nombre de pinochet, está subido al depósito de CRAN. Para empezar, instalemos este paquete junto con el paquete rnaturalearthhires, que nos proporciona la forma de todos los países del mundo desde la página web de Natural Earth Data’s:
install.packages("pinochet")
install.packages("rnaturalearthhires",
repos="http://packages.ropensci.org", type = "source")Tip: El paquete
rnaturalearthhirespuede ser de gran utilidad si se posee una base de datos con variables que puedan ser comparadas entre países, usando las técnicas que ya se han aprendido.
A continuación, filtraremos la base de datos para seleccionar Chile y sus países vecinos:
chile <- rnaturalearthhires::countries10 %>%
st_as_sf() %>%
filter(SOVEREIGNT %in% c("Chile", "Argentina", "Peru", "Bolivia"))A continuación, cargamos la base de datos pinochet y seleccionamos las variables que se utilizarán, que corresponden al tipo de lugar donde la víctima fue atacada, así como la latitud y la longitud del lugar. También contiene una descripción de los lugares, que se utilizará más adelante en un ejercicio.
pinochet <- pinochet::pinochet %>%
select(last_name, first_name, place_1, longitude_1, latitude_1,
location_1)
head(pinochet)
## last_name first_name place_1 longitude_1 latitude_1
## 1 Corredera Reyes Mercedes del Pilar In Public -71 -34
## 2 Torres Torres Benito Heriberto Home -71 -33
## 3 Lira Morales Juan Manuel In Public -71 -33
## location_1
## 1 Calle Gran Avenida
## 2 Santiago
## 3 La Legua shantytown
## [ reached 'max' / getOption("max.print") -- omitted 3 rows ]Luego, usamos la función st_as_sf() para transformar las variables de longitud y latitud en geometrías del tipo sf. El argumento crs representa el tipo de Sistema de Referencia de Coordenadas (CRS, por sus siglas en inglés) según su código llamado EPSG. En este caso, utilizaremos el código “4326,” que corresponde al estándar WGS84, el más común. Por otro lado, usamos el comando remove = F para que la función no elimine las variables originales de latitud y longitud de la base de datos, de tal forma que se pueda usar para generar puntos con geom_points. También eliminaremos previamente los valores NA.
Tip: Cuando repliques este ejercicio, ten en cuenta que en el argumento
coordssiempre tienes que poner primero la longitud y la latitud. De lo contrario, tus variables pueden quedar con sus coordenadas invertidas.
pinochet_sf <- pinochet %>%
filter(place_1 != "NA" & !is.na(longitude_1) & !is.na(latitude_1)) %>%
st_as_sf(coords = c("longitude_1", "latitude_1"), crs = 4326, remove = F)
head(pinochet_sf)
## Simple feature collection with 6 features and 6 fields
## geometry type: POINT
## dimension: XY
## bbox: xmin: -71 ymin: -34 xmax: -71 ymax: -33
## geographic CRS: WGS 84
## last_name first_name place_1 longitude_1 latitude_1
## 1 Corredera Reyes Mercedes del Pilar In Public -71 -34
## 2 Torres Torres Benito Heriberto Home -71 -33
## location_1 geometry
## 1 Calle Gran Avenida POINT (-71 -34)
## 2 Santiago POINT (-71 -33)
## [ reached 'max' / getOption("max.print") -- omitted 4 rows ]
class(pinochet_sf)
## [1] "sf" "data.frame"Observa que con esta acción hemos transformado la base de datos en un shapefile.
A continuación, generamos el mapa con geom_sf, usándolo en dos instancias: primero, para mapear los polígonos de los países, y segundo, para graficar los puntos espaciales. Usamos el atributo size para el tamaño del punto. Considera que usamos el argumento coords_sf para delimitar el área que se mostrará en el mapa. Haciendo esto, también podemos identificar las víctimas atacadas fuera del territorio nacional de Chile, sin perder el foco en este país.
ggplot() +
geom_sf(data = chile) +
geom_sf(data = pinochet_sf, size = 1) +
coord_sf(xlim = c(-75.6, -67), ylim = c(-55, -19)) +
scale_x_continuous(breaks = c(-76, -67)) # también limpiar la escala x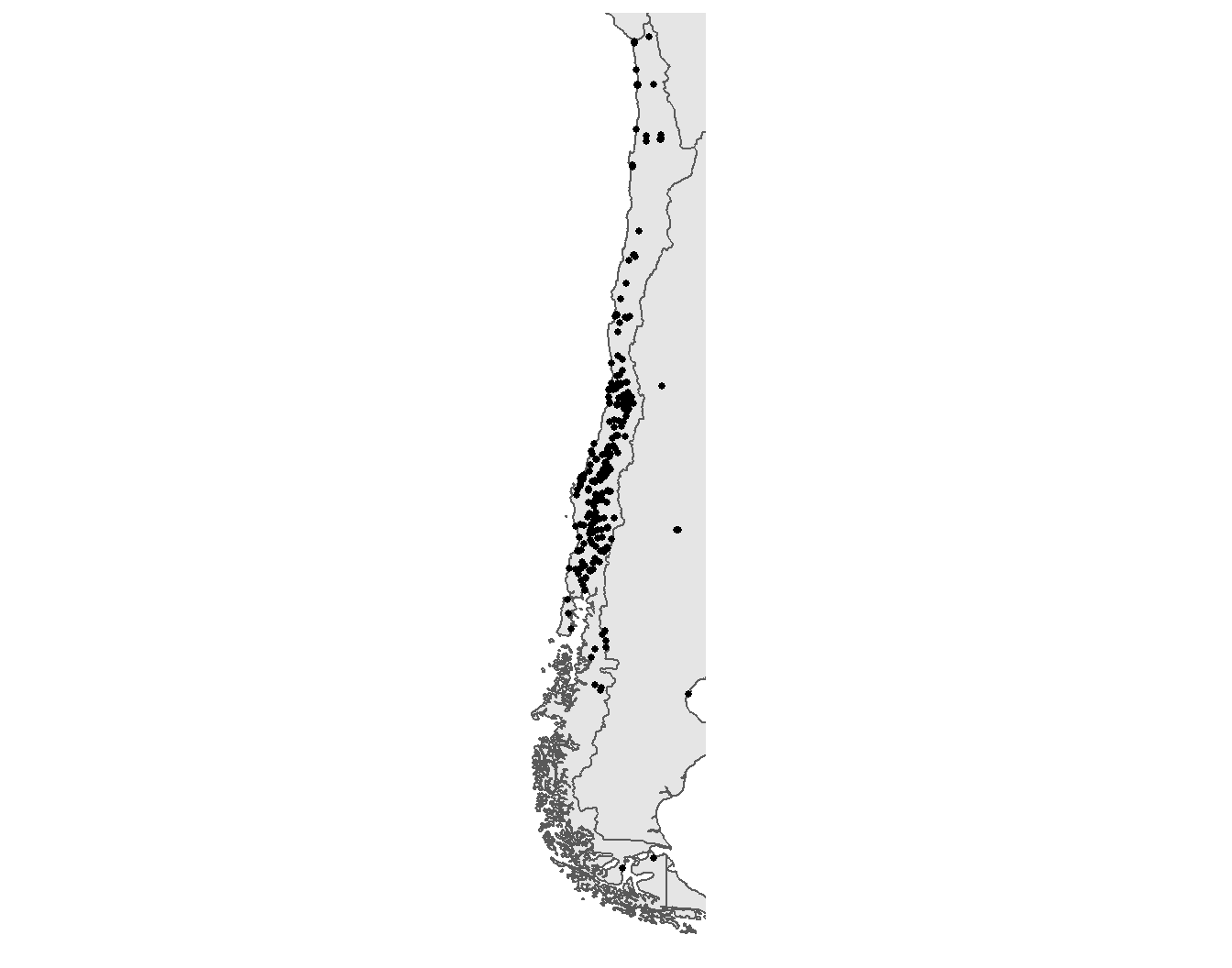
Figura 3.27: Mapa de la ubicación de las víctimas de la dictadura de Pinochet en Chile y sus países vecinos
Podemos obtener un resultado similar con geom_point(). En este caso, añadimos el argumento color = para mostrar el tipo de lugar donde la víctima fue atacada.
ggplot() +
geom_sf(data = chile) +
geom_sf(data = pinochet_sf,
mapping = aes(color = place_1),
size = 1) +
coord_sf(xlim = c(-75.6, -67), ylim = c(-55, -19)) +
scale_x_continuous(breaks = c(-76, -67)) +
labs(color = "") # también limpiar la escala x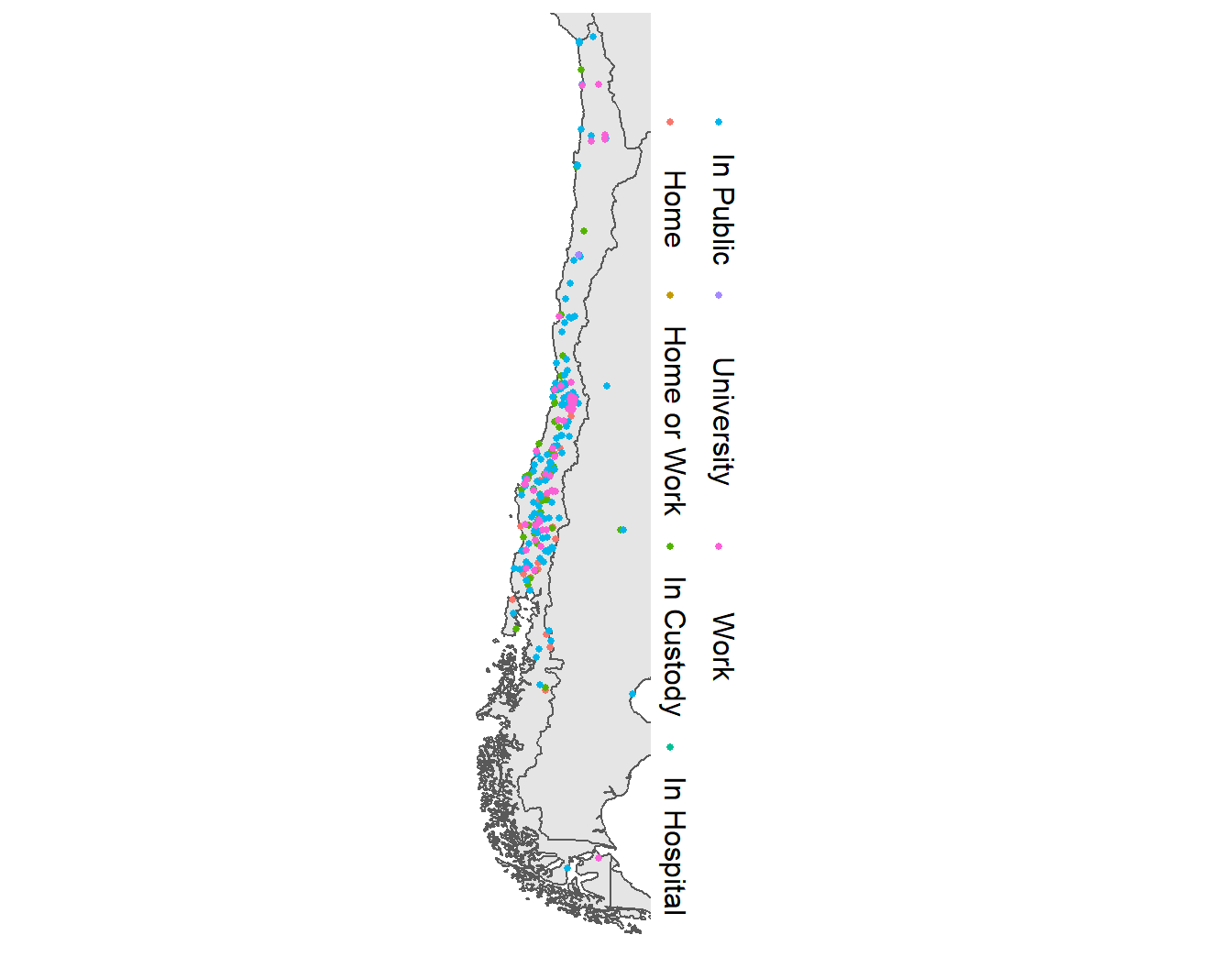
Figura 3.28: Mapa de la ubicación de las víctimas de la dictadura de Pinochet en Chile y sus países vecinos, codificado por color según el tipo de lugar
Ejercicio 16C.
- Generar centroides para los países (Tip: usar
CNTRY_NAME).- Generar un mapa usando el argumento
filldeggplot()para usar un color diferente para cada país.- Grafique un mapa combinando los atributos de los dos ejercicios anteriores.
- Crear un mapa con el PIB per cápita (
e_migdppc) de cada país en el año 2016. ¿Cuáles son los países que no tienen datos para el 2016?- Crear una tabla con el valor de Democracia (
v2x_polyarchy) de cada país en los años 2013, 2014, 2015 y 2016.
16.5 Inferencia a partir de datos espaciales
Más allá del análisis exploratorio y descriptivo que se puede hacer con los datos espaciales, éstos son también de gran utilidad para hacer inferencias sobre la relación de varios fenómenos. La inferencia basada en los datos espaciales parte del reconocimiento de que las observaciones espaciales no pueden asumirse como mutuamente independientes, ya que las observaciones que están cerca unas de otras tienden a ser similares. Por lo tanto, debemos prestar mucha atención a las diferentes pautas de asociación que existen en los fenómenos que estamos estudiando.
Estas pautas espaciales (autocorrelación espacial), miden la influencia de la distancia sobre una determinada variable, y pueden utilizarse como información relevante de los tipos de influencia que aún no se han observado o considerado (R. S. Bivand, Pebesma, and Gómez-Rubio 2013, 11).
16.5.1 Indicador local de asociación espacial (LISA, por sus siglas en inglés)
En esta sección encontrarás los mecanismos básicos para entrar en la correlación espacial, basados en el Indicador Local de Asociación Espacial (LISA), introducido por Luc Anselin (1995). Éstos permiten indicar la similitud (correlación) existente entre observaciones cercanas entre sí, es decir, si están agrupadas en cluster espacialmente. Para ello, Anselin indica que:
- El LISA para cada observación da un indicador del grado de agrupación espacial significativa de valores similares alrededor de esa observación.
- La suma de los LISA de las observaciones es proporcional a un indicador de correlación espacial global.
Mediante la prueba de la significancia estadística de estos indicadores podemos identificar los lugares en los que hay un grado significativo de clusterización (Brunsdon and Comber 2015, 249). Se dice que las variables tienen una correlación espacial positiva cuando los valores similares tienden a estar más cerca unos de otros que los valores diferentes (Lansley and Cheshire 2016, 77)
16.5.2 Matriz de pesos espaciales
El primer paso para hacer este tipo de análisis es determinar el conjunto de vecindarios para cada observación, es decir, identificar los polígonos que comparten fronteras entre ellos. Luego, necesitamos asignar un peso para cada relación de vecindad, lo que permite definir la fuerza de esta relación basada en la proximidad. En las matrices de pesos, los vecinos se definen de forma binaria [0,1] en cada fila, indicando si existe o no una relación.
Para hacer este tipo de análisis, primero tenemos que cargar el paquete spdep, y guardar las coordenadas de las unidades en nuestro mapa:
library(spdep)coords <- coordinates(as((shp_brasil), 'Spatial'))En esta sección, también trabajaremos con el shapefile al que hemos añadido datos de la base de datos de Freire (2018), shp_brasil_data, pero sólo utilizaremos los datos del último año disponible, 2009:
shp_brasil_data <- shp_brasil_data %>% filter(anio == 2009)Hay tres criterios diferentes para calcular los barrios:
16.5.2.1 El criterio Rook (de la torre)
El criterio Rook considera como vecinos a cualquier par de células que compartan un borde. Piensa en una torre en un tablero de ajedrez.
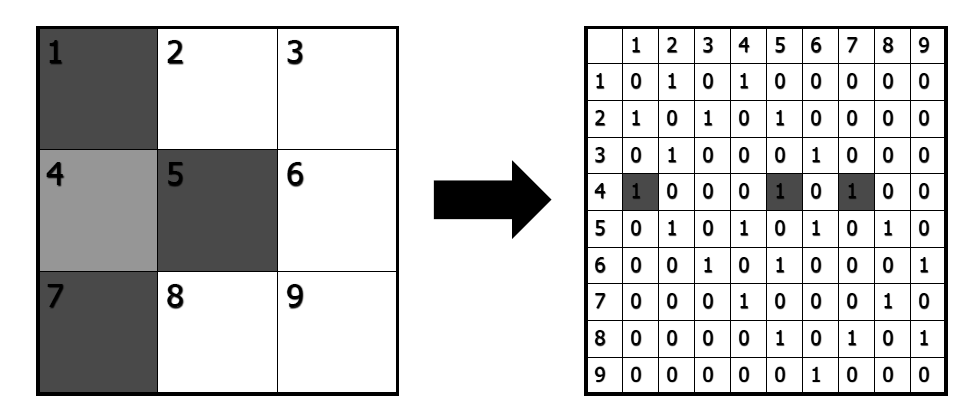
Figura 16.4: El criterio Rook de vecindad
Para generar este criterio, usamos la función poly2nb() del paquete spdep. Tenemos que asegurarnos de que el argumento queen = está configurado como F.
rook_brasil <- poly2nb(as(shp_brasil_data, 'Spatial'), queen = FALSE)Podemos graficar esto sobre nuestro mapa con ggplot(). Primero, necesitamos pasar nuestras coordenadas a un marco de datos con esta función de Maxwell B. Joseph.
nb_to_df <- function(nb, coords){
x <- coords[, 1]
y <- coords[, 2]
n <- length(nb)
cardnb <- card(nb)
i <- rep(1:n, cardnb)
j <- unlist(nb)
return(data.frame(x = x[i], xend = x[j],
y = y[i], yend = y[j]))
}Generamos el dataframe:
rook_brasil_df <- nb_to_df(rook_brasil, coords)Ahora, podemos generar el gráfico con geom_point() y geom_segment():
ggplot(shp_brasil_data) +
geom_sf()+
geom_point(data = rook_brasil_df,
mapping = aes(x = x, y = y))+
geom_segment(data = rook_brasil_df,
mapping = aes(x = x, xend = xend, y = y, yend = yend))+
labs(x = "",y = "")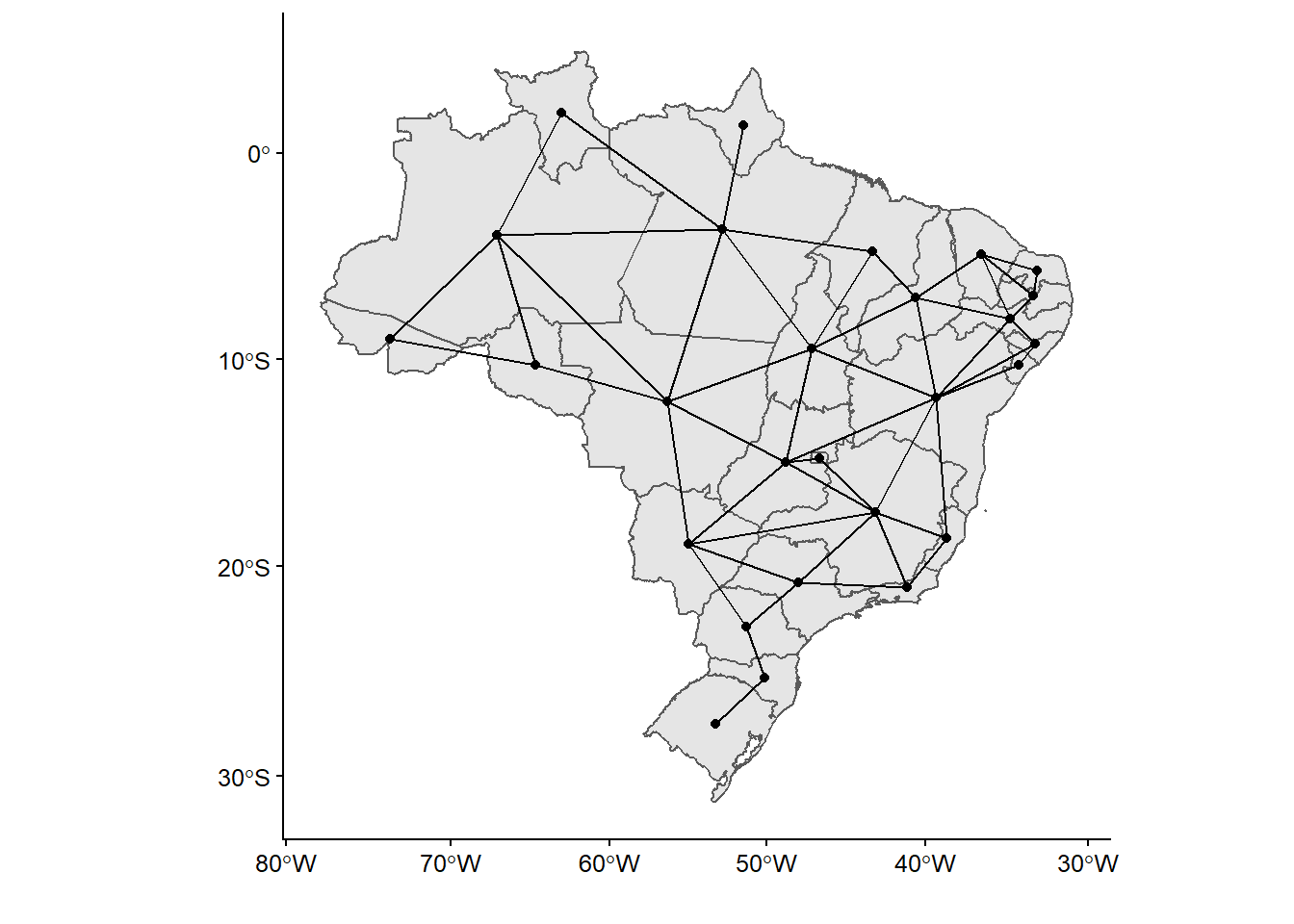
Figura 5.13: El criterio Rook de vecindad en Brasil
16.5.2.2 Criterio Queen (de la Reina)
El criterio de la reina considera como vecinos a cualquier par de celdas que compartan un borde o un vértice.
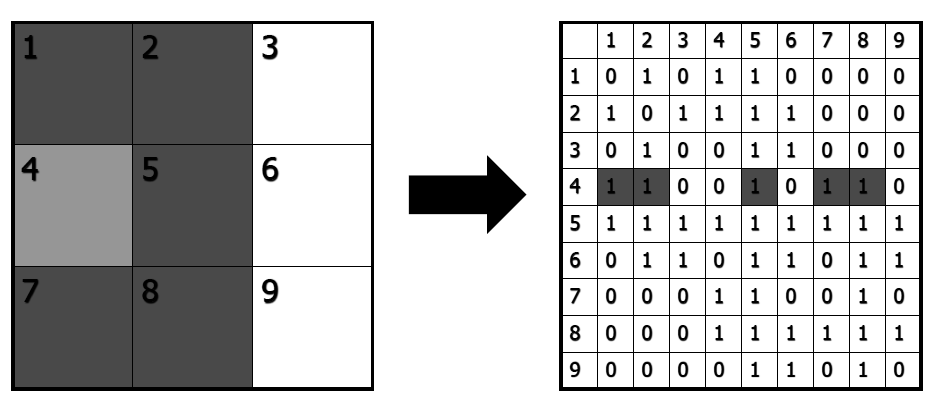
Figura 16.5: El criterio Queen de vecindad
Para generar este criterio, también usamos la función poly2nb(), y después el dataframe:
queen_brasil <- poly2nb(as(shp_brasil_data, 'Spatial'), queen = T)
queen_brasil_df <- nb_to_df(queen_brasil, coords)Ahora podemos generar el gráfico, lo cual hacemos directamente sobre nuestro mapa de Brasil:
ggplot(shp_brasil_data) +
geom_sf()+
geom_point(data = queen_brasil_df,
mapping = aes(x = x, y = y))+
geom_segment(data = queen_brasil_df,
mapping = aes(x = x, xend = xend, y = y, yend = yend))+
labs(x = "", y = "")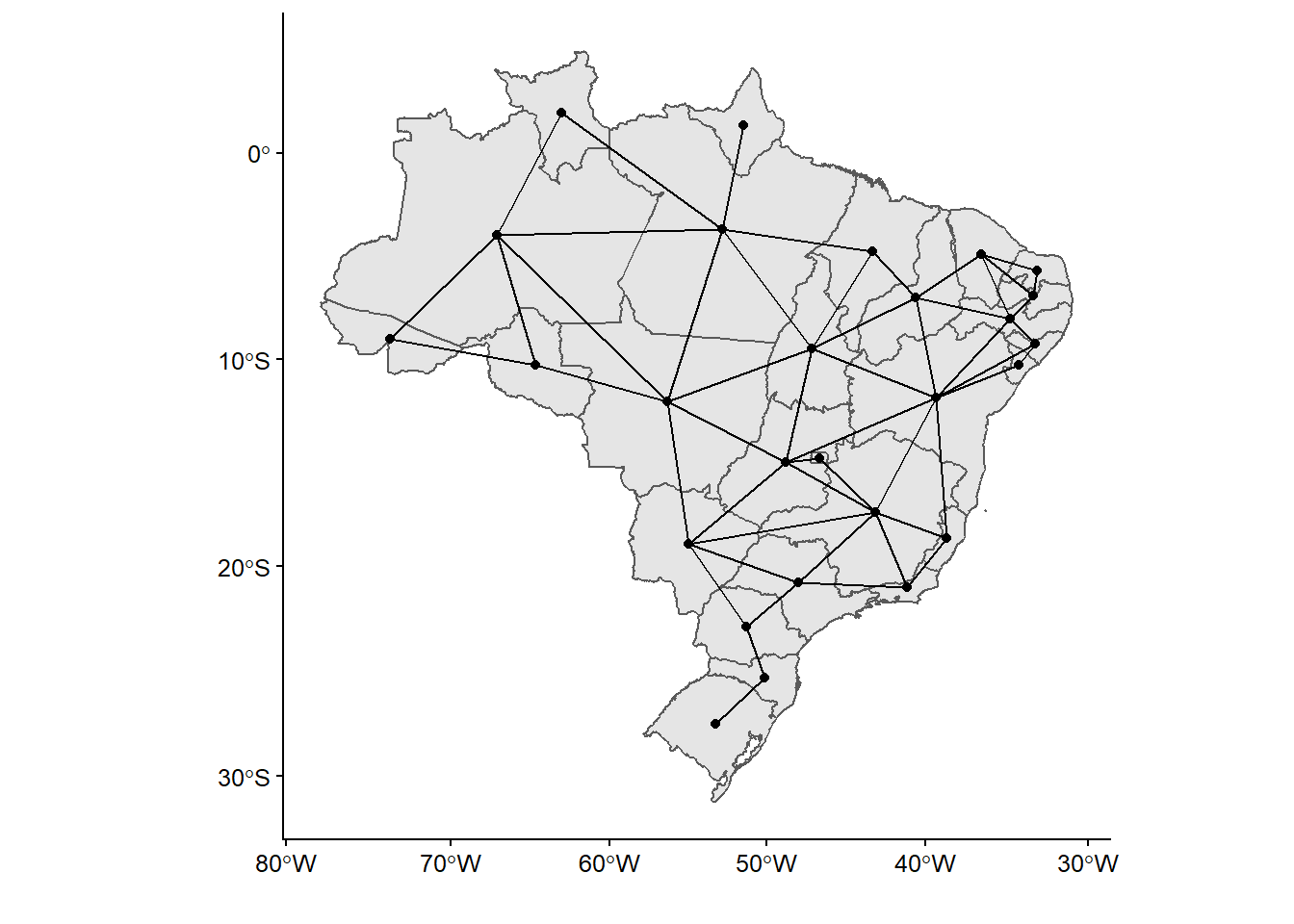
Figura 16.6: El criterio Rook de vecindad en Brasil
16.5.2.3 Criterio k-cercanos (K-nearest)
En el criterio K-más cercano se generan barrios basados en la distancia entre vecinos, donde ‘k’ se refiere al número de vecinos de un lugar en particular, calculado como la distancia entre los puntos centrales de los polígonos. Se suele aplicar cuando las áreas tienen diferentes tamaños, de modo que cada ubicación contiene el mismo número de vecinos, independientemente del tamaño de las áreas vecinas (Fuente: https://geodacenter.github.io/glossary.html).
En este caso, usaremos los seis vecinos más cercanos. Podemos hacerlo con el comando knn2nb. También generamos inmediatamente el dataframe:
kn_brasil <- knn2nb(knearneigh(coords, k = 6))
kn_brasil_df <- nb_to_df(kn_brasil,coords)Entonces, genera el mapa con ggplot():
ggplot(shp_brasil_data) +
geom_sf()+
geom_point(data = kn_brasil_df, mapping = aes(x = x, y = y))+
geom_segment(data = kn_brasil_df,
mapping = aes(x = x, xend = xend, y = y, yend = yend))+
labs(x = "", y = "")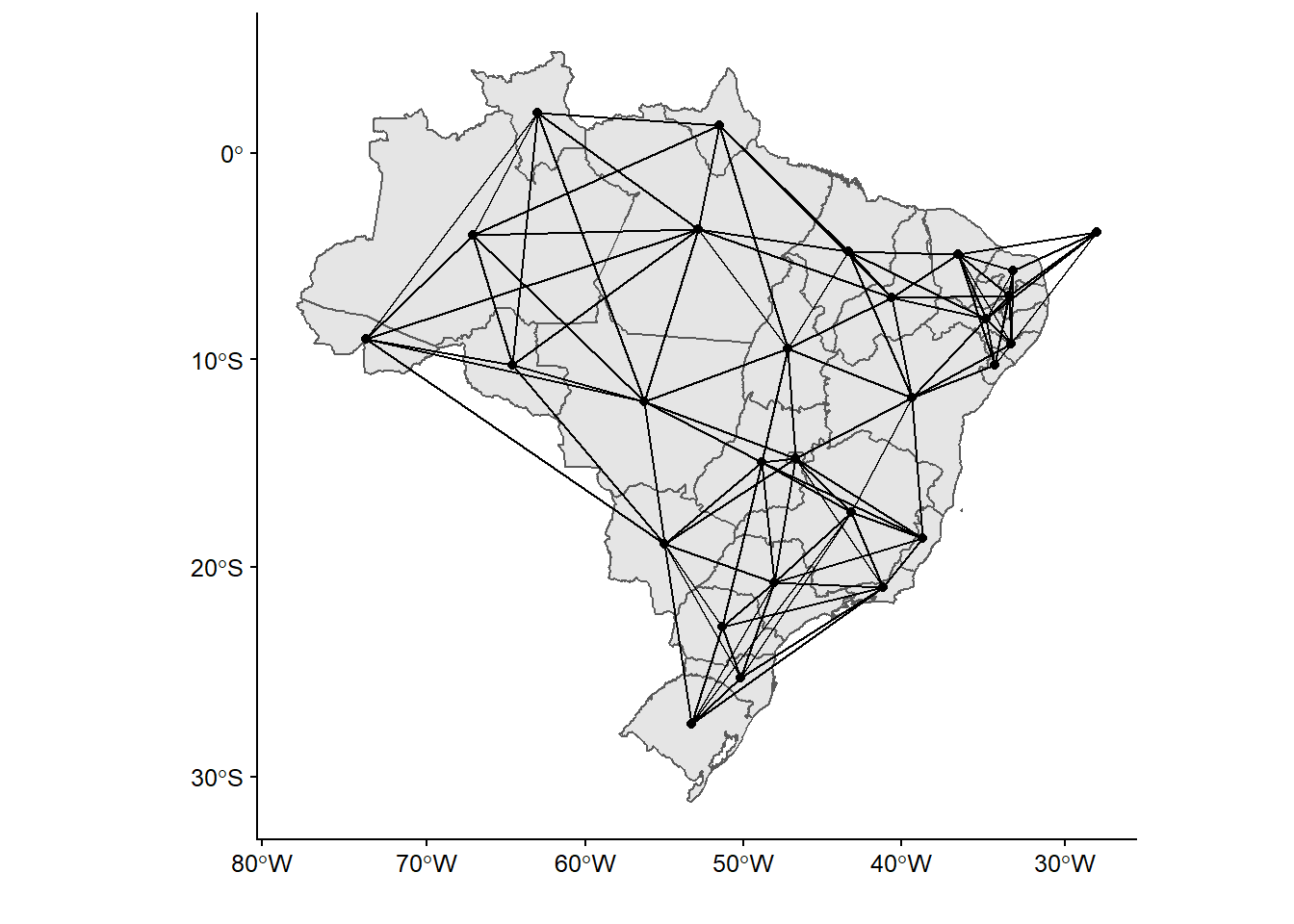
Figura 16.7: Mapa de los vecinos, criterio de cercanía
Obsérvese que, mientras que Rook y Queen generan, para nuestro caso, resultados similares en términos de vecindad en nuestro mapa, el modelo de k-cercanos añade muchas más relaciones.
16.5.3 I de Moran
La I de Moran es la estadística más utilizada para identificar la correlación espacial:
\[ I = \frac{n}{\sum_{i=1}^{n}(yi - \bar{y})^2} \frac{\sum_{i=1}^{n}\sum_{j=1}^{n}wij(yi - \bar{y})(yj - \bar{y})}{\sum_{i=1}^{n}\sum_{j=1}^{n}wij}\]
Esta fórmula, aunque parece compleja, no es más que una versión ampliada de la fórmula para calcular el coeficiente de correlación, a la que se añade una matriz de peso espacial69. A través de ella, podemos probar y visualizar la presencia de la autocorrelación espacial. Primero, haremos una prueba global que crea una única medida de correlación espacial. Este test de Moran crea una correlación entre -1 y 1, en la que:
1 determina una perfecta correlación espacial positiva (indica que nuestros datos están agrupados en clusters).
0 significa que nuestros datos están distribuidos aleatoriamente.
-1 representa una correlación espacial negativa (valores disímiles que están cerca unos de otros).
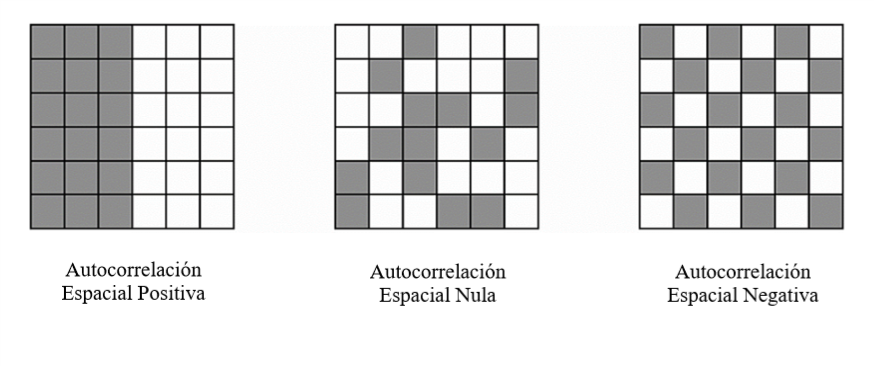
Figura 16.8: Ilustración de la autocorrelación espacial
Utilizando una simulación de Monte Carlo, en la que los valores se asignan aleatoriamente a los polígonos para calcular el I de Moran, la simulación se repite muchas veces para establecer una distribución de los valores esperados. Después de esto, el valor del I de Moran observado se compara con la distribución simulada para ver cuán probable es que los valores observados puedan considerarse aleatorios, lo que permite determinar si existe una autocorrelación espacial significativa (RSpatial).
Para ejecutar el test del I de Moran utilizamos el comando moran.test. La variable para la que diagnosticaremos la correlación espacial es el índice de Gini, y utilizaremos un criterio Queen. Antes, necesitamos generar un objeto tipo listw (matriz de peso), basado en el criterio Queen.
queen_brasil_lw <- nb2listw(queen_brasil)Con este objeto podemos ejecutar el test I de Moran, donde seleccionamos la matriz de peso que acabamos de crear:
moran.test(shp_brasil_data$gini, listw = queen_brasil_lw)
##
## Moran I test under randomisation
##
## data: shp_brasil_data$gini
## weights: queen_brasil_lw
##
## Moran I statistic standard deviate = 2, p-value = 0.01
## alternative hypothesis: greater
## sample estimates:
## Moran I statistic Expectation Variance
## 0.284 -0.038 0.020El resultado del test I de Moran muestra que hay una ligera relación de correlación positiva, frente a la expectativa de una ligera relación negativa. Sin embargo, el test resulta no ser estadísticamente significativo, ya que tiene un valor p inferior a un umbral de significativo de 0,05. Por lo tanto, podemos indicar que la tasa de homicidios no presenta altos grados de autocorrelación espacial al analizar estos datos a nivel estatal en Brasil. Lo más probable es que muestre una correlación espacial si utilizamos una unidad de análisis más pequeña (microrregiones dentro de los estados, por ejemplo).
También creamos un gráfico de dispersión para visualizar el signo y la fuerza de la correlación espacial. Para generar un gráfico de dispersión utilizamos el comando moran.plot():
moran.plot(shp_brasil_data$ratio_homicidios, listw = queen_brasil_lw,
xlab = "Tasa de homicidios",
ylab = "Tasa de homicidios (con corr. espacial)")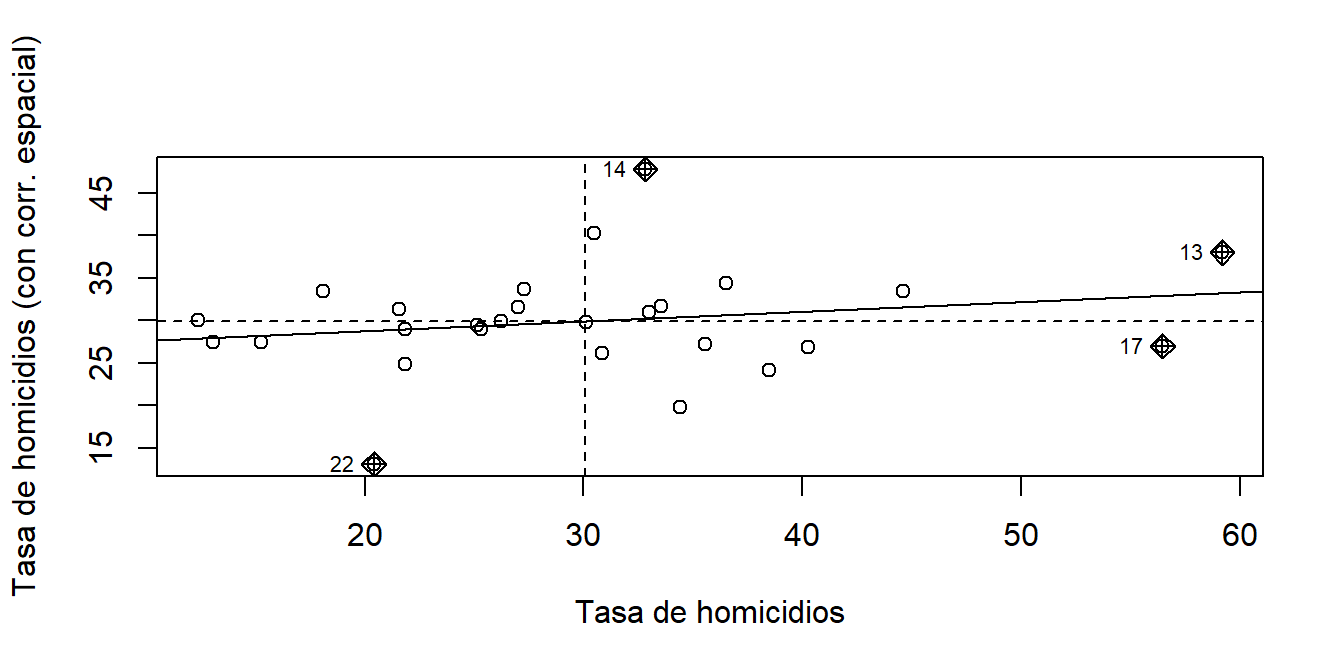
Figura 16.9: Correlación espacial del índice de Gini en Brasil a nivel estatal
En este mapa, la línea sólida del gráfico indica el valor del I de Moran, es decir, la medida global de autocorrelación espacial en nuestros datos. Como vimos en la prueba anterior, es ligeramente positivo. El eje horizontal del gráfico muestra los datos de la tasa de homicidios a nivel estatal en Brasil, y el eje vertical muestra los mismos datos, pero con retraso espacial. Los cuatro cuadrantes del gráfico describen el valor de la observación en relación con sus vecinos: alto-alto, bajo-bajo (autocorrelación espacial positiva), bajo-alto o alto-bajo (autocorrelación espacial negativa), y el gráfico también señala los valores considerados atípicos en esta relación, como el Distrito Federal o Acre.70
Si bien el test I de Moran nos permite identificar la existencia de clusters a nivel global, no permite identificar si existen clusters locales significativos en la variable que estamos analizando (Lansley and Cheshire 2016, 78). Por eso queremos hacer un test I de Moran a nivel local, donde se calculan los indicadores locales de asociación espacial para cada unidad de nuestros datos, y se prueba la relación para probar su significancia estadística. Esto nos da datos sobre el patrón geográfico de la relación de los datos espaciales, y si hay desviaciones locales de los patrones globales de autocorrelación espacial.
Después de crear un nuevo listw de objeto de vecinos, este tipo con el argumento style = "B" para indicar una clasificación binaria, utilizamos localmoran() para ejecutar el test I de Moran. Añadimos sus resultados (estimación y valor p) a nuestro objeto sf existente con el conocido mutate():
queen_brasil_b_lw <- nb2listw(queen_brasil, style = "B")
shp_brasil_data <- shp_brasil_data %>%
mutate(lmoran = localmoran(x = gini, listw = queen_brasil_b_lw)[, 1],
lmoran_pval = localmoran(x = gini, listw = queen_brasil_b_lw)[, 5]
)A continuación, mapeamos los resultados con ggplot2:
ggplot(shp_brasil_data) +
geom_sf(aes(fill = lmoran))+
labs(fill = " Estadística local de Moran") +
scale_fill_viridis_c()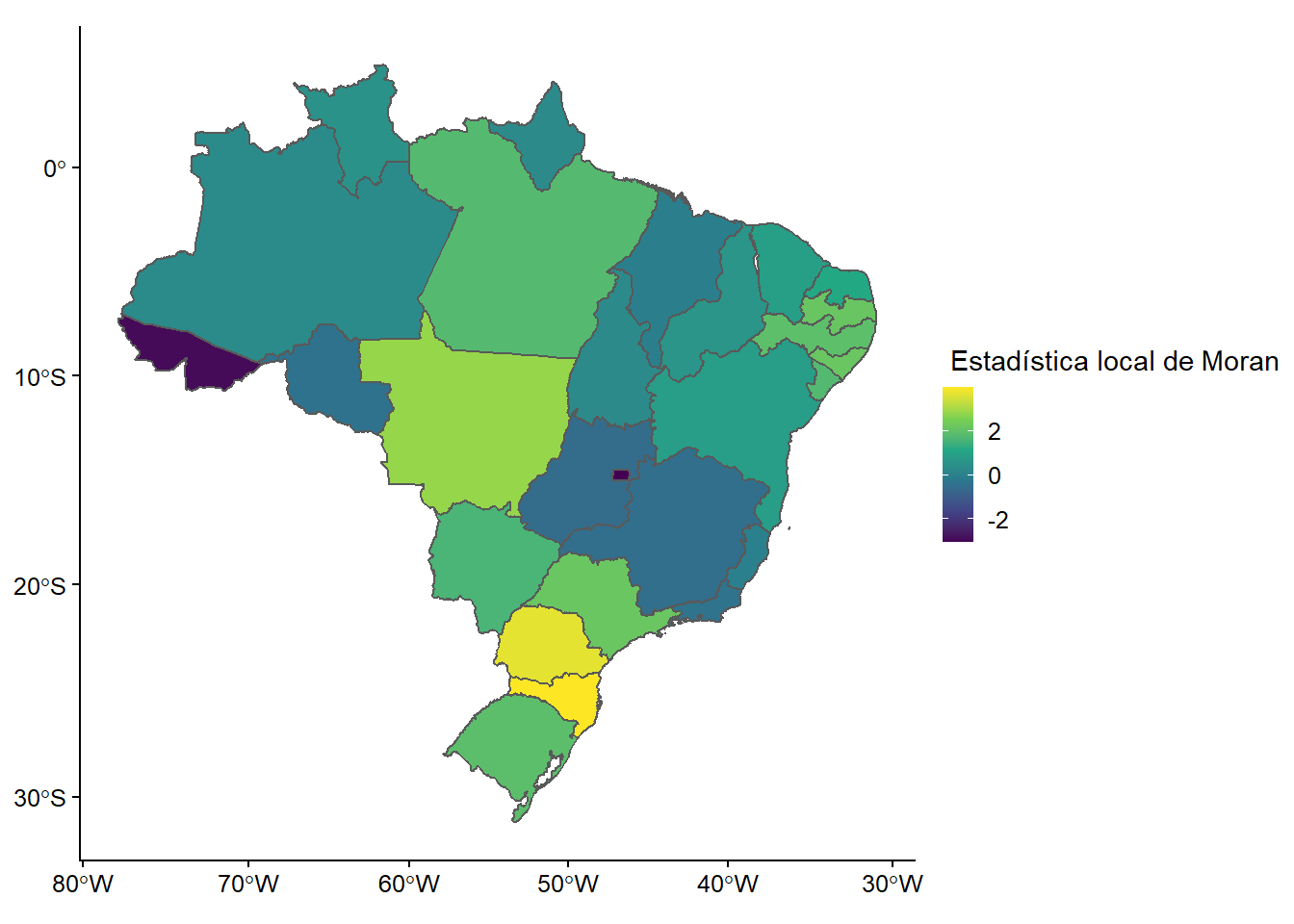
Figura 11.6: El test de Moran a nivel local para diferentes valores de Gini
Este mapa nos permite observar la variación de la autocorrelación en todo el espacio, pero no permite identificar si los patrones de autocorrelación son cúmulos con valores altos o bajos. Esto permitiría analizar el tipo de autocorrelación espacial que existe y su significado. Para ello necesitamos crear un mapa de clusters LISA, el cual creará una etiqueta basada en los tipos de relación que comparte con sus vecinos (alto-alto, bajo-alto, insignificante, etc.) en concordancia con los valores de la variable que estamos analizando (Gini).
Para ello, necesitamos hacer una serie de transformaciones que detallamos a continuación:
shp_brasil_data <- shp_brasil_data %>%
mutate(
# Estandarizar el Gini y el Moran local a sus valores medios:
st_gini = gini - mean(gini),
st_lmoran = lmoran - mean(lmoran),
# Crear la nueva variable categórica:
cuadrante = case_when(
lmoran_pval > 0.05 ~ "Insignificante",
st_gini > 0 & st_lmoran > 0 ~ "Alto-Alto",
st_gini < 0 & st_lmoran < 0 ~ "Bajo-Bajo",
st_gini < 0 & st_lmoran > 0 ~ "Bajo-Alto",
st_gini > 0 & st_lmoran < 0 ~ "Alto-Bajo"
)
)Ahora podemos generar el gráfico con ggplot(). Nota que usamos scale_fill_manual() para cambiar los colores para que reflejen la intensidad de la autocorrelación:
ggplot(shp_brasil_data, aes(fill = cuadrante)) +
geom_sf()+
labs(fill = "Cuadrante")+
scale_fill_manual(values = c("red", "lightblue", "white"))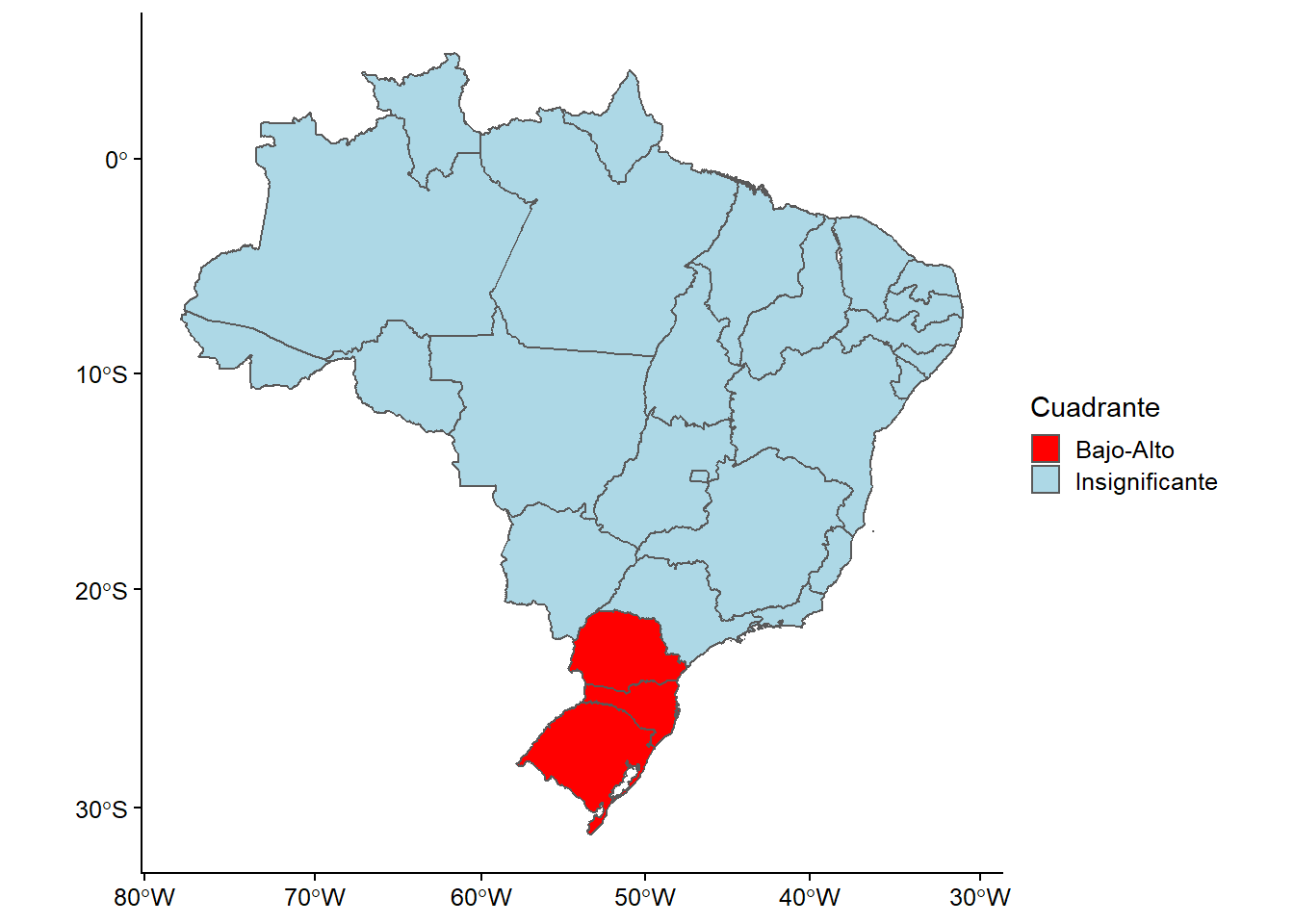
Figura 16.10: Patrones geográficos de agrupación para diferentes valores de Gini
Este mapa nos proporciona mayor información sobre los patrones geográficos de autocorrelación espacial. Este mapa nos muestra la existencia de clusters; por lo tanto, muestra regiones agrupadas en lugar de ubicaciones individuales. Es importante señalar que estos mapas no son significativos, pero nos permiten encontrar ubicaciones o relaciones que pueden ser interesantes para un análisis más profundo.
En este caso, podemos interpretar que en la mayor parte de Brasil no existe una correlación espacial para los valores de Gini a nivel estatal, es decir, su valor no está influenciado por la proximidad de otros valores similares. Sin embargo, en algunos estados situados en el noreste de Brasil, podemos observar la existencia de un cluster donde se concentran altos valores de Gini, que tienen vecinos que también tienen altos valores en la misma variable (puntos calientes). Esto indica que estas regiones contribuyen significativamente a una autocorrelación espacial positiva global. Por otro lado, en los estados que están coloreados en azul claro encontramos clusters que concentran valores bajos de Gini donde sus vecinos tienen valores altos de las mismas variables y, por lo tanto, contribuyen significativamente a una autocorrelación espacial global negativa (ya que esto ocurre cuando los valores disímiles están próximos entre sí).
Ejercicio 16D.
Genera y objeta con las coordenadas del shapefile usando la función
coordinates().Filtra la base de datos para usar sólo los datos del 2018.
Genera una matriz de peso siguiendo el criterio Queen usando
poly2nb. Genera el marco de datos usandonb_to_df()y grafícalo usandogeom_point()ygeom_segment().Realiza el test I de Moran con el comando
moran.test()usando la base de datos y la variable de Democracia Electoral. Grafícalo usandomoran.plot().Realiza el test I de Moran local con el comando
localmoran(usa los parámetros del ejercicio anterior), átalo al conjunto de datos concbind()y grafica el resultado conggplot().
Comentarios finales: Referencias para un mejor análisis de datos espaciales
Como dijimos al principio, el objetivo de este capítulo era hacer una introducción al análisis de datos espaciales en R, centrándose en la creación de mapas como un valioso instrumento para el análisis descriptivo de los datos políticos. Sin embargo, el análisis de los datos espaciales no comienza ni termina con lo que se explicó en este capítulo. Si estás interesado en aprender más sobre ciertos temas como el aprendizaje estadístico y el modelado de bases de datos geográficos, la interacción con otros softwares de análisis de datos geográficos como QGIS, y la aplicación de éstos en áreas como el transporte o la ecología, le recomendamos que eches un vistazo a Geocomputación en R (Lovelace, Nowosad, and Münchow 2019), un libro donde encontrarás una guía de introducción a estos temas. También te recomendamos mirar en el envoltorio de R highcharter para la librería de JavaScript Highcharts si quieres encontrar nuevas formas de visualizar los datos espaciales y crear mapas más complejos.
E-mail: abescobar@uc.cl↩︎
E-mail: goortiz@uc.cl↩︎
Las características simples se refieren a un estándar de formato (ISO 19125-1:2004) que describe cómo los objetos del mundo real pueden ser representados en las computadoras. Ver r-spatial.github.io/sf/articles/sf1.html.↩︎
Para más información, consulta https://github.com/r-spatial/sf#installling↩︎
Puede que veas las coordenadas en los ejes. Esto puede ser útil para análisis exploratorio de datos, pero deberías eliminarlos si quieres compartir tu mapa, lo que se puede realizar añadiendo
... + theme_void()↩︎Si en tu trabajo encuentras que esto no es así, deberás usar la herramienta de unión fuzzy que mostramos en el capítulo de manejo avanzado de datos.↩︎