Capítulo 6 Selección de casos basada en regresiones

Inés Fynn²⁸ y Lihuen Nocetto²⁹

Lecturas sugeridas

Gerring, J. (2006). Case Study Research: Principles and Practices. Cambridge: Cambridge University Press.
Lieberman, E. S. (2005). Nested analysis as a mixed-method strategy for comparative research. American Political Science Review, 99(3), 435-452.
Seawright, J. (2016). Multi-Method Social Science: Combining Qualitative and Quantitative Tools. Cambridge: Cambridge University Press.

Los paquetes que necesitas instalar

tidyverse (Wickham 2019b), paqueteadp (Urdinez and Cruz 2020), broom (Robinson and Hayes 2020).

6.1 Selección de estudios de casos

Este capítulo le dará herramientas para, a partir de lo que hemos aprendido en el capítulo de los modelos lineales, utilizar las regresiones para seleccionar los estudios de casos. Estas técnicas serán útiles cuando se haga una investigación con métodos mixtos. Cuando trabajamos con datos de observación (en contraposición a los experimentales) las regresiones lineales no pueden, por sí mismas, responder a las preguntas de inferencia causal.³⁰. Es decir, aunque pueden desvelar la existencia de una relación entre nuestras variables independientes y dependientes, nuestra investigación estaría incompleta si no somos capaces de demostrar, a través de otros métodos, cómo estas variables están causalmente conectadas. Un excelente libro para consultar y aprender más sobre este tema es " Multi-Method Social Science" de Jason Seawright (2016).

La selección del método está guiada por la pregunta que queremos responder. Por ejemplo, si nuestro interés es entender cuáles son las causas de la desigualdad en América Latina y el Caribe, utilizaríamos un análisis estadístico de n-grande que nos permitiría analizar el mayor número de países posible. De esta manera, en el capítulo 5 encontramos que, en promedio, el gasto educativo tiene un efecto positivo sobre los niveles de desigualdad. Sin embargo, el descubrimiento de que un mayor gasto genera mayores niveles de desigualdad resulta un tanto intrigante y contrario a la intuición. Un hallazgo como éste podría tener importantes repercusiones en la elaboración de políticas públicas y consecuencias para la vida cotidiana de las personas.

Por lo tanto, para avanzar en nuestra investigación es deseable responder, por ejemplo, ¿Por qué la educación afecta positivamente a los niveles de desigualdad? Es decir, cuál es el mecanismo causal que explica que en América Latina y el Caribe un mayor gasto en educación genere mayores niveles de desigualdad. Para responder a este tipo de preguntas, solemos recurrir a métodos cualitativos (como estudios de caso en profundidad o análisis de rastreo de procesos³¹ que nos permite comprender cuáles son los tipos de procesos que explican por qué y cómo se produce la relación causal. De esta manera, lo que intentamos hacer es integrar (Seawright 2016) dos métodos de investigación, en los que un método plantea la pregunta de investigación (derivada del análisis estadístico), y el otro busca responderla (a través de un estudio de caso). Otra alternativa para reforzar nuestra investigación podría ser a través de la triangulación, es decir, abordar la misma pregunta de investigación pero desde diferentes métodos que, tomados en su conjunto, pueden generar una respuesta más compleja y completa de nuestra pregunta de investigación.

A pesar de su elección (integración o triangulación), el objetivo de un diseño de método de investigación mixto es combinar diferentes métodos para alcanzar una explicación más compleja de los fenómenos que estamos estudiando. El objetivo de los métodos mixtos es precisamente abordar los mismos fenómenos a través de diferentes metodologías que permitan captar diferentes ángulos o dimensiones de un problema de investigación. Aunque existen infinitas formas de combinar los métodos, algunos métodos son más compatibles entre sí que otros y, de hecho, algunas combinaciones pueden causar más confusión que claridad (Lieberman 2005).

En esta sección, aprenderemos una combinación de métodos que Lieberman (2005) ha llamado análisis anidado (nested analysis), que es la combinación del análisis estadístico de una gran muestra con el estudio en profundidad de uno o más casos contenidos en esa muestra. En resumen, lo que haremos es seleccionar casos (en este caso, países) a partir de la estimación de nuestro modelo.

Después de estimar el modelo, el primer paso para seleccionar los casos es estimar los residuos y los valores predichos del modelo para cada una de nuestras observaciones. Esto se debe a que, para seleccionar nuestros casos de estudio, compararemos lo que nuestro modelo predijo con los valores observados de cada uno de estos casos.

Para obtener los residuos y los valores predichos en R utilizaremos el comando augment del paquete broom. Este comando crea una nueva base de datos sobre el modelo que añade variables a la base de datos original (para cada observación): valores predichos, errores estándar, los residuos y residuos estandarizados, entre otras estadísticas. Usaremos el modelo 2 que estimamos en el capítulo 5 con datos de Huber et al. (2006) como ejemplo.

Residuos y valores predichos:

library(tidyverse)
library(broom)

library(paqueteadp)
data("bienestar")

bienestar_sinna <- bienestar %>% 
  drop_na(gini, gasto_educ, inversion_extranjera, gasto_salud, gasto_segsocial, 
          poblacion, dualismo_sectorial, diversidad_etnica, pib, tipo_regimen, 
          bal_legislativo, represion)

model_2 <- lm(gini ~ 1 + gasto_educ + inversion_extranjera + gasto_salud + gasto_segsocial + poblacion 
              + dualismo_sectorial + diversidad_etnica + pib +  tipo_regimen + bal_legislativo +
                 represion,
               data = bienestar_sinna)

model_aug <- broom::augment(model_2, data = bienestar_sinna)
model_aug
## # A tibble: 167 x 21
##   pais  codigo_pais  anio poblacion  gini dualismo_sector~   pib
##   <chr> <chr>       <dbl>     <dbl> <dbl>            <dbl> <dbl>
## 1 Arge~ ARG          1982      30.8  40.2             9.50 7711.
## 2 Arge~ ARG          1983      30.9  40.4             8.36 7907.
## 3 Arge~ ARG          1990      30.7  43.1             7.72 6823.
## # ... with 164 more rows, and 14 more variables

6.2 ¿Qué estudio de caso debería seleccionar para la investigación cualitativa?

Los casos seleccionados para un estudio cualitativo en profundidad se eligen de una población, y las razones de su selección dependen de su representatividad dentro de esa población. En este sentido, según (Gerring 2006), un estudio de caso no puede existir aislado de un análisis de casos cruzados relativamente grande. Su mejor estudio de caso dependerá de cuál es el objetivo para el que se seleccionó el caso. De esta manera, la selección del caso debe ser intencional y no aleatoria (Gerring 2006). A continuación, se presentan diferentes objetivos para los cuales se seleccionan y se implementan los casos en R, basados en nuestro modelo estadístico sobre los determinantes de la desigualdad en América Latina y el Caribe.

6.2.1 Casos típicos

Uno de los objetivos de la selección de casos es examinar con mayor detalle los mecanismos que conectan la variable independiente con la variable dependiente. Si este es nuestro objetivo, entonces queremos seleccionar casos que sean ejemplos típicos de las relaciones que encontramos en el análisis estadístico. Por lo tanto, lo que buscamos es un caso con el menor residuo posible. Es decir, el caso en que nuestro modelo predijo el mejor. Estos son también llamados casos sobre la línea (casos que están sobre la línea de regresión).

Para identificar este caso graficaremos, usando la base de datos creada con la función augment(), los residuos. Los transformaremos en valor absoluto porque, por defecto, siempre hay residuos negativos. Además, para identificar los casos, pediremos a ggplot() que añada las etiquetas de los cuatro (top_n(-4. -resid_abs)) países (mapping = aes(label = pais)) con los residuos más bajos. Incorporamos la línea horizontal (geom_hline(aes(yintercept = 0))) al gráfico para visualizar dónde los residuos son casi nulos (allí se encuentran los casos que el modelo predijo perfectamente: es decir, el caso típico).

ggplot(data = model_aug, mapping = aes(x = .fitted, y = .resid)) +
  geom_point() +
  geom_hline(aes(yintercept = 0)) +
  geom_text(data = model_aug %>% 
              mutate(.resid_abs = abs(.resid)) %>% 
              top_n(-4, .resid_abs),
            mapping = aes(label = pais))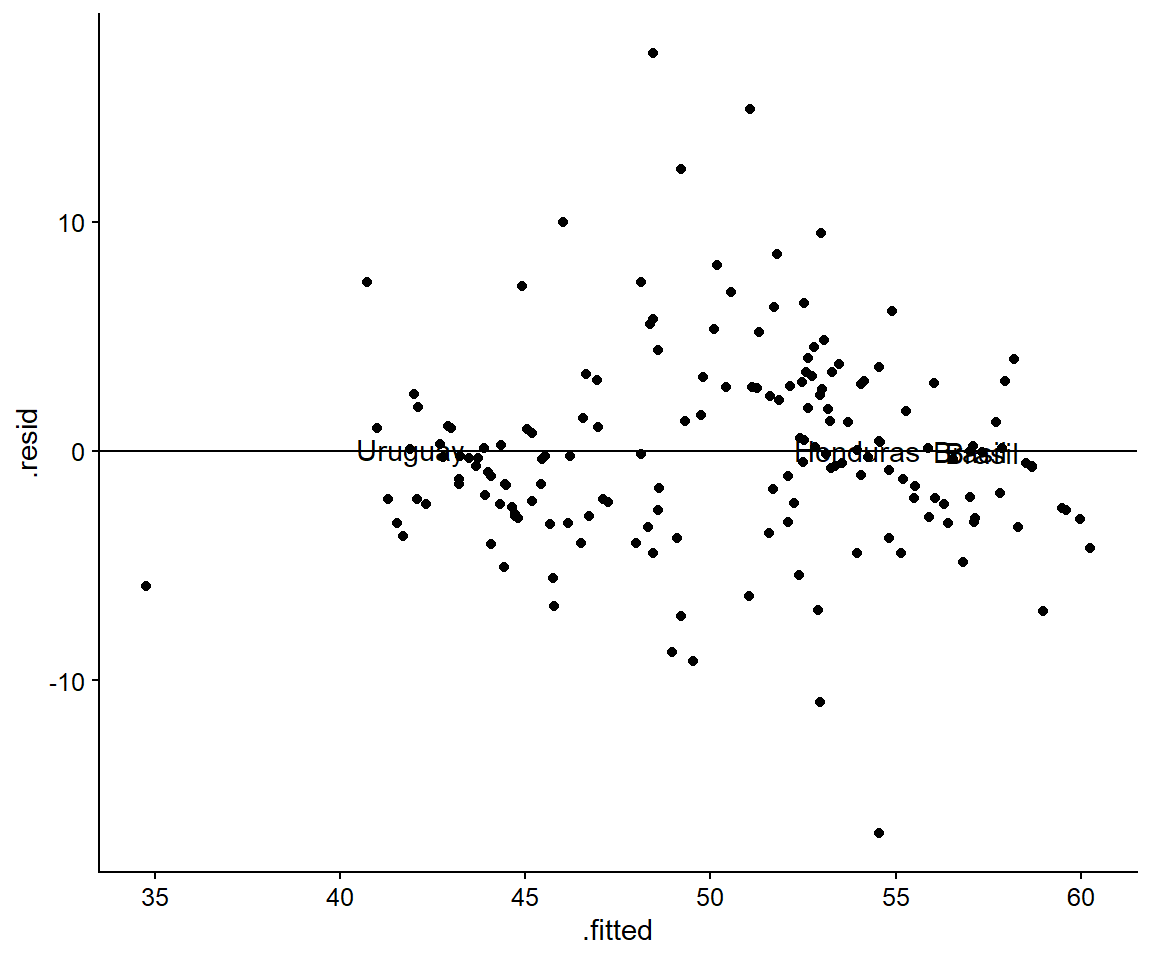

Figura 3.3: Los 4 casos típicos más importantes

Según el gráfico, el Brasil (dos veces), Honduras y el Uruguay son tres casos típicos del modelo estimado sobre los determinantes de la desigualdad en América Latina y el Caribe. Es decir, se trata de casos que explican sus niveles de desigualdad en base a las variables del Modelo 2, ya sea que la desigualdad sea alta (Brasil, Honduras) o baja (Uruguay).

6.2.2 Los valores atípicos

Los valores atípicos son casos que, dado nuestro modelo, presentan un comportamiento no esperado; son valores atípicos porque no pueden ser bien explicados a través de nuestro modelo. En resumen, son “anomalías teóricas” (Gerring 2006, 106). En general, seleccionamos estos tipos de casos para explorar nuevas hipótesis, que pueden eventualmente arrojar luz sobre las variables omitidas en el modelo estadístico. La selección de los valores atípicos funciona de manera opuesta a la selección de los casos típicos: en lugar de seleccionar los que tienen el residuo más bajo, queremos seleccionar los casos cuyo valor predicho difiere más del valor real (es decir, que tienen los residuos más altos).

ggplot(data = model_aug, 
       mapping = aes(x = .fitted, y = .resid)) +
  geom_point() +
  geom_hline(aes(yintercept = 0)) +
  geom_text(data = model_aug %>% 
              mutate(.resid_abs = abs(.resid)) %>% 
              top_n(4, .resid_abs),
            mapping = aes(label = pais))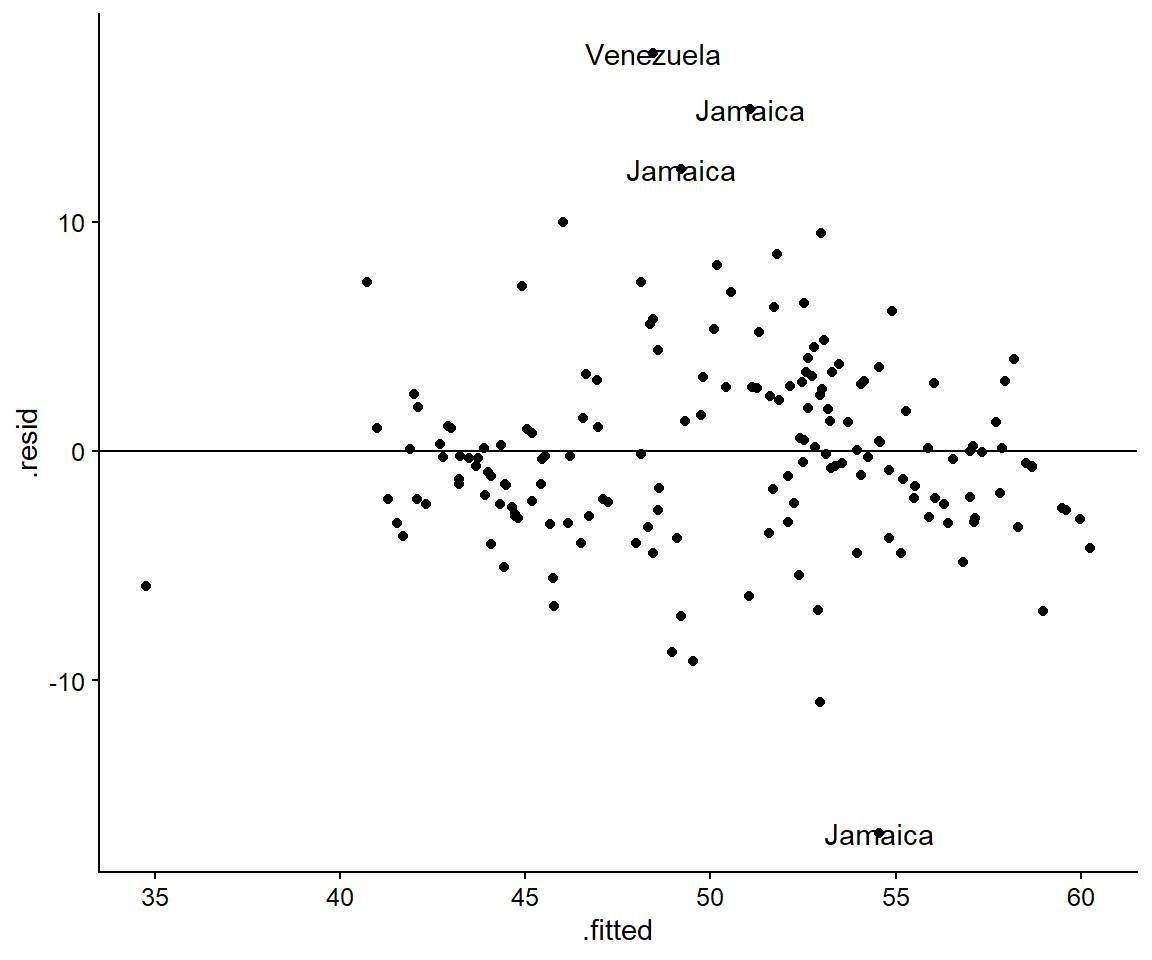

Figura 3.4: Los 4 principales casos atípicos

Jamaica (en varios años) aparece como un país mal explicado por nuestro modelo. Es un país que presenta niveles relativamente bajos de desigualdad, pero las variables independientes del modelo no dan cuenta de estos valores. Hay un año especialmente interesante, 1993, en el que su puntuación de Gini es de 35,7, lo que la convierte en una de las más equitativas de la muestra. Rodeado de algunos de los más desiguales países del mundo tendríamos que añadir una nueva variable a nuestro modelo para explicar el caso de Jamaica.

6.2.3 Casos influyentes

Los casos influyentes son aquellos que presentan valores extremos ya sea en las variables independientes y tienen una fuerte influencia en la regresión. Es decir, son casos que influyen fuertemente en la pendiente de la regresión que observamos (recordemos que la pendiente viene dada por el coeficiente de regresión \(\beta_i\)). Estos son casos que, como valores atípicos, también son “inusuales.” Mientras que la selección de un valor atípico se utiliza para explorar hipótesis alternativas, la selección de un caso influyente ayuda a confirmar nuestra hipótesis de base (Gerring 2006). Para identificar los casos influyentes, podemos tomar dos caminos:

Por un lado, podemos utilizar los dfbetas, que son estadísticas que indican cuánto cambia el coeficiente de regresión \(\beta_i\) en unidades de desviación estándar si la i-th observación fuera borrada. Por lo tanto, tendremos un dfbeta por cada observación que indica cuánto cambiaría el \(\beta_i\) de la variable gasto_educ (gasto en educación) si no se incluyera esta observación en la muestra. Así, cuanto más varíe la pendiente (\(\beta_i\)) con la ausencia de la observación, más influyente será esa observación.

A continuación, queremos seleccionar los casos que producen mayores cambios en la desviación estándar de \(\beta_i\) cuando se eliminan de la muestra. Como mencionamos, los casos influyentes se utilizan para confirmar nuestras teorías. Al mismo tiempo, si la eliminación de las observaciones influyentes de la muestra anula las relaciones que habíamos encontrado (si al eliminar el caso \(\beta_i\) deja de ser significativo), estos casos también son útiles para explorar nuevas hipótesis o identificar las variables que se omitieron en el modelo.

model_aug %>%
  mutate(dfb_cseduc = as.tibble(dfbetas(model_2))$gasto_educ) %>%
  arrange(-dfb_cseduc) %>%
  slice(1:3) %>%
  dplyr::select(pais, dfb_cseduc)
## Warning: Problem with `mutate()` input `dfb_cseduc`.
## i `as.tibble()` is deprecated as of tibble 2.0.0.
## Please use `as_tibble()` instead.
## The signature and semantics have changed, see `?as_tibble`.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.
## i Input `dfb_cseduc` is `as.tibble(dfbetas(model_2))$gasto_educ`.
## Warning: `as.tibble()` is deprecated as of tibble 2.0.0.
## Please use `as_tibble()` instead.
## The signature and semantics have changed, see `?as_tibble`.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.
## # A tibble: 3 x 2
##   pais      dfb_cseduc
##   <chr>          <dbl>
## 1 Barbados       0.483
## 2 Jamaica        0.298
## 3 Venezuela      0.241

Usando la distancia de Cook, que se basa en una lógica similar a la de dfbetas. La distancia de Cook considera los valores que cada observación asume para las variables independientes y dependientes para calcular cuánto varían los coeficientes cuando cada observación está ausente de la muestra. En resumen, esta distancia nos dice cuánto influye cada observación en la regresión en su conjunto: cuanto mayor es la distancia de Cook, mayor es la contribución de la observación a las inferencias del modelo. Los casos con mayor distancia de Cook son centrales para mantener las conclusiones analíticas (especialmente con muestras relativamente pequeñas; con muestras grandes es menos probable que existan casos con tal influencia). Por lo tanto, el uso de la distancia de Cook para seleccionar casos para un estudio en profundidad puede ser relevante: si en el estudio cualitativo de un caso influyente no podemos confirmar nuestra teoría, es poco probable que podamos confirmarla en otros casos.

ggplot(data = model_aug,
       mapping = aes(x = .fitted, y = .cooksd)) +
  geom_point() +
  geom_text(data = model_aug %>% top_n(3, .cooksd),
            mapping = aes(label = pais)) +
  labs(title = " Casos influyentes")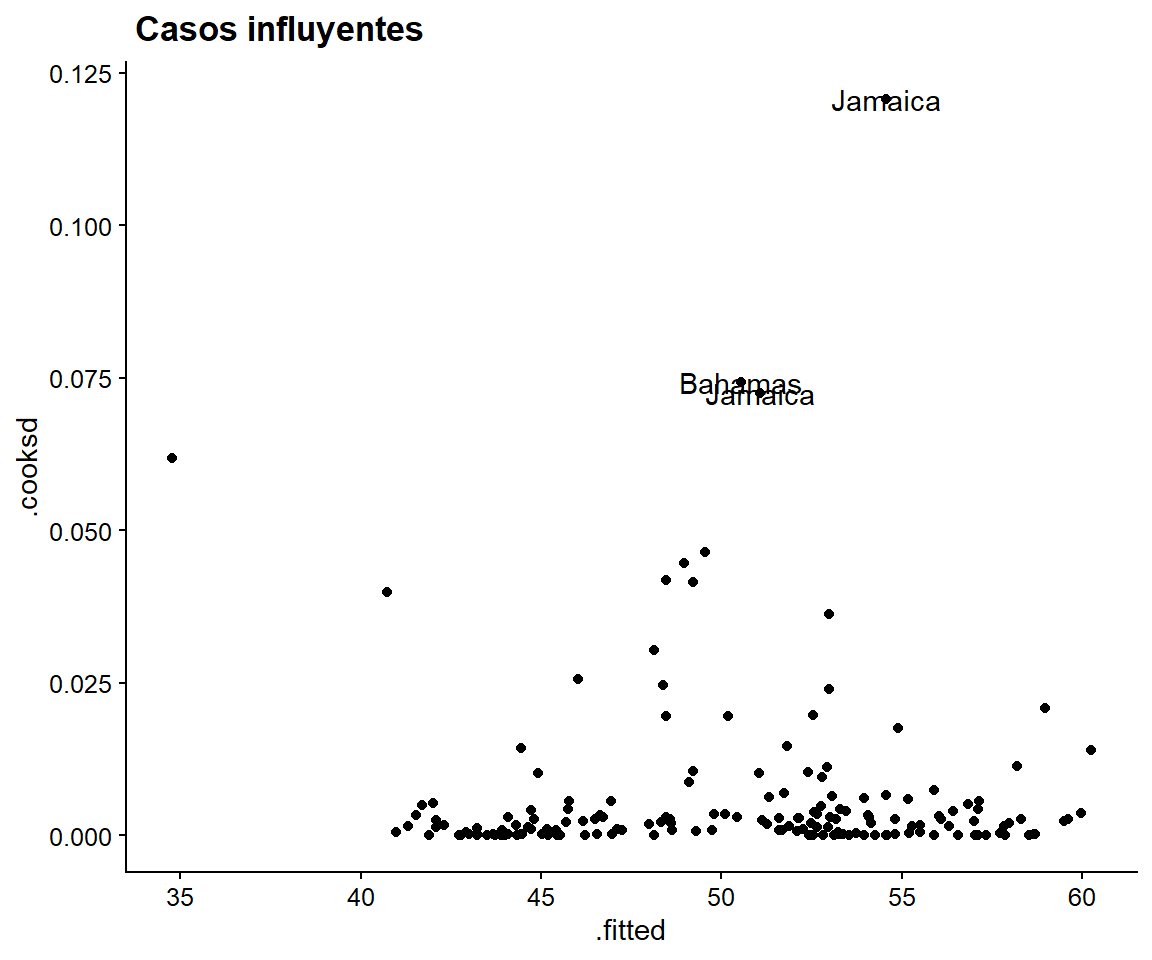

Figura 3.6: Los 3 casos más influyentes

Una vez más, Jamaica se destaca como un país para ser estudiado en profundidad.³²

6.2.4 Casos extremos

La selección de los casos extremos implica la identificación de observaciones que se ubican lejos de la media de la distribución de la variable independiente o dependiente. La utilidad de estas observaciones radica en la “rareza” de sus valores. Esta técnica se recomienda cuando no existe un supuesto teórico sólido y, por lo tanto, la investigación se centra en la construcción teórica. El estudio en profundidad de los casos extremos es más bien exploratorio: es una forma de evaluar y buscar las posibles causas de \(y\) o los posibles efectos de \(x\). Es importante señalar que un caso extremo puede coincidir tanto con un caso típico como con un caso atípico (Gerring 2006).

Un trabajo clásico de selección de casos extremos en la variable dependiente es el de Theda Skocpol (1979) sobre revoluciones sociales, donde la teoría se desarrolla en base a tres casos que presentan el valor más extremo para una revolución (de hecho, son los únicos que presentan tal valor según Skocpol).

6.2.4.1 Casos extremos en la variable independiente: \(x\)

Observemos cómo se comporta la variable independiente:

ggplot(bienestar_sinna, aes(x = gasto_educ)) +
  geom_histogram(binwidth = 1,color="white", fill="black") +
  labs(
    subtitle = "% del PIB gastado en Educación",
    caption = "Fuente: Huber et al (2006))",
    x = "Gasto en educación",
    y = "Frecuencia"
  )

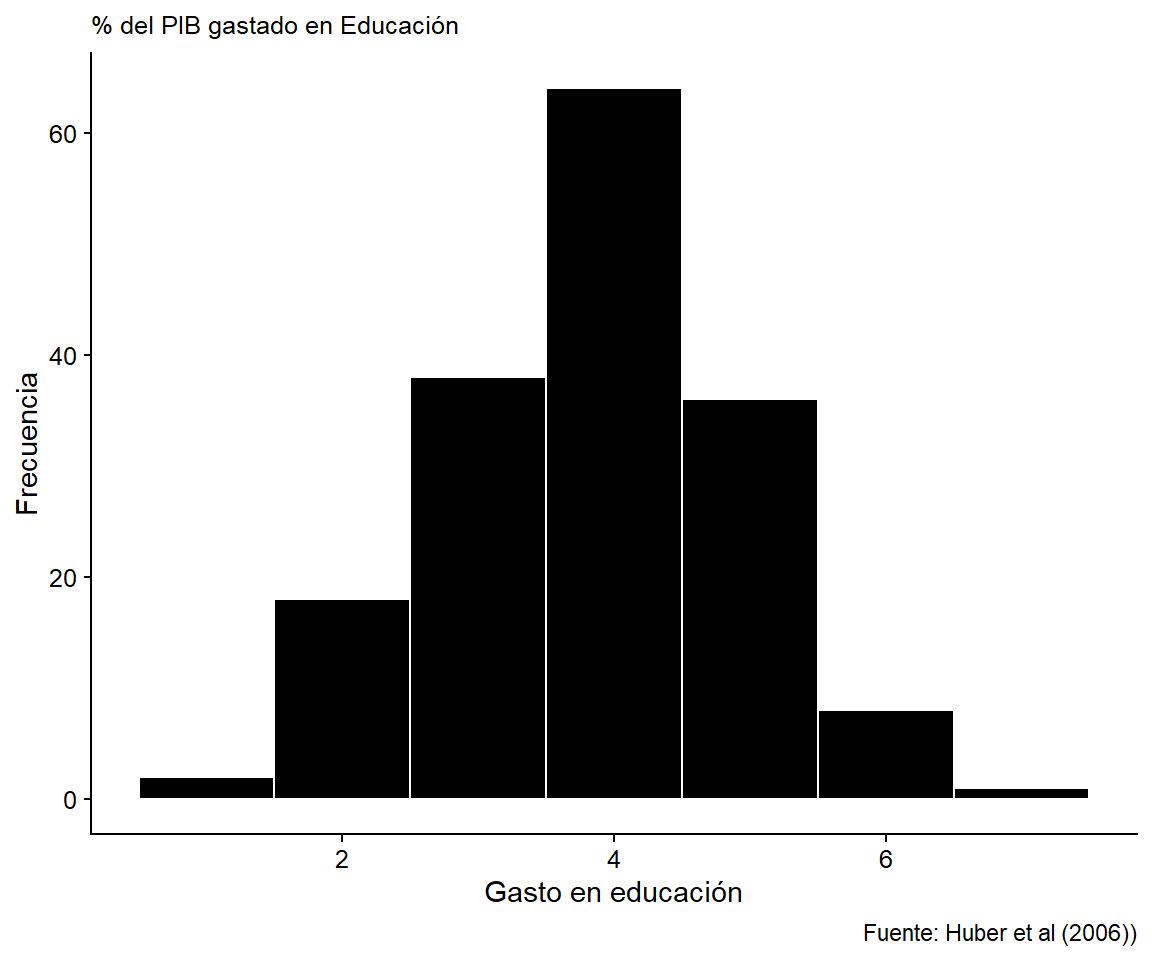
Figura 3.7: Histograma de la Variable Independiente: Gastos de educación

Para la selección de casos extremos sobre la variable independiente, a partir del modelo estadístico estimado, sólo hay que calcular la diferencia -en valores absolutos- entre el valor de cada observación y la media muestral del gasto en educación. Luego, se seleccionan los tres casos que presentan la mayor diferencia con la media de la muestra.

Estos pasos se implementan en R de la siguiente manera:

mean(model_aug$gasto_educ, na.rm = T)
## [1] 4

model_aug %>%
  mutate(dif_cseduc = abs(gasto_educ - mean(gasto_educ, na.rm = T))) %>%
  top_n(3, dif_cseduc) %>%
  arrange(-dif_cseduc) %>%
  dplyr::select(pais, anio, gasto_educ, dif_cseduc)
## # A tibble: 3 x 4
##   pais      anio gasto_educ dif_cseduc
##   <chr>    <dbl>      <dbl>      <dbl>
## 1 Barbados  1981        0.8       3.16
## 2 Honduras  2001        6.8       2.84
## 3 Uruguay   1984        1.4       2.56

Graficamos los resultados para una mejor visualización:

model_aug <- model_aug %>% 
  mutate(dif_cseduc = abs(gasto_educ - mean(gasto_educ, na.rm = T)))

ggplot(data = model_aug,
       mapping = aes(x = .fitted, y = dif_cseduc)) +
  geom_point() +
  geom_text(data = model_aug %>% top_n(3, dif_cseduc),
            mapping = aes(label = pais))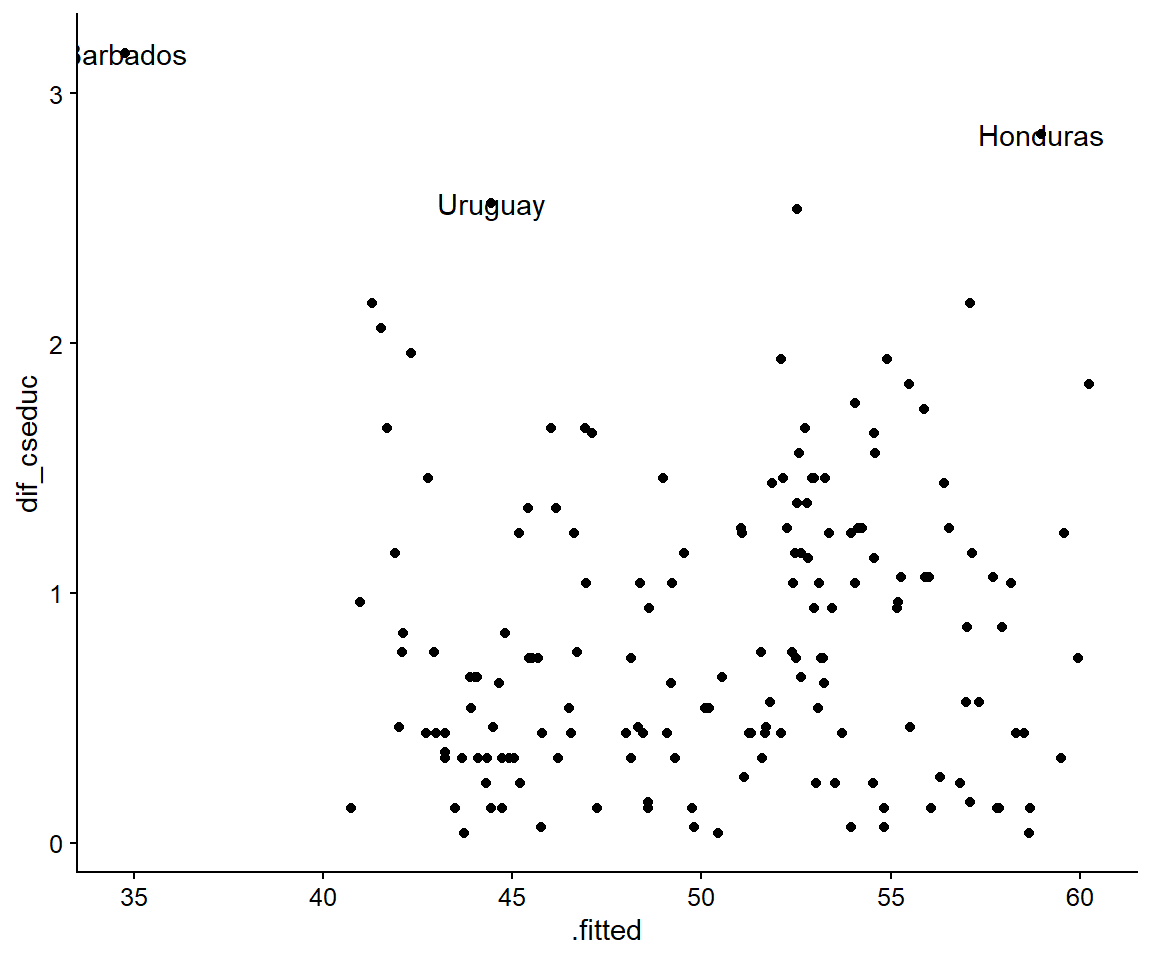

Figura 3.9: Los tres casos extremos más importantes en los gastos de educación

Barbados se destaca por ser un caso extremo, ya que está muy por debajo de la media de la muestra. Honduras, por el contrario, está muy por encima. Sería interesante comparar ambos. Considerando que el tercer país es Uruguay, y que los tres son economías relativamente pequeñas, surge una pregunta que seguramente nos hará mejorar el modelo: ¿no deberíamos controlar por el tamaño de la economía, medido por su PIB? Esta duda podría llevarnos a un nuevo modelo, donde la significancia estadística podría cambiar.

Ejercicio 6A. Seleccione los casos extremos para la variable independiente Inversión Extranjera Directa inversion_extranjera.

6.2.4.2 Casos extremos en la variable dependiente \(y\)

La selección de los casos extremos en la variable dependiente se hace de la misma manera que con los casos extremos en \(x\). La única diferencia es que ahora calculamos la diferencia -en valores absolutos- entre el valor observado de cada observación y la media de la muestra en la variable dependiente (Índice de Gini, en este ejemplo). Luego, se seleccionan los tres casos que presentan la mayor diferencia entre la media de la muestra y su valor de la variable dependiente.

mean(model_aug$gini, na.rm = T)
## [1] 50

model_aug %>%
  mutate(dif_gini = abs(gini - mean(gini, na.rm = T))) %>%
  top_n(3, dif_gini) %>%
  arrange(-dif_gini) %>%
  dplyr::select(pais, gini, dif_gini)
## # A tibble: 3 x 3
##   pais       gini dif_gini
##   <chr>     <dbl>    <dbl>
## 1 Barbados   28.9     21.4
## 2 Jamaica    66       15.7
## 3 Venezuela  65.8     15.5

También podemos graficarlo para una mejor visualización:

model_aug <- model_aug %>% 
  mutate(dif_gini = abs(gini - mean(gini, na.rm = T)))

ggplot(data = model_aug, 
       mapping = aes(x = .fitted, y = dif_gini)) +
  geom_point() +
  geom_text(data = model_aug %>% top_n(2, dif_gini),
            mapping = aes(label = pais))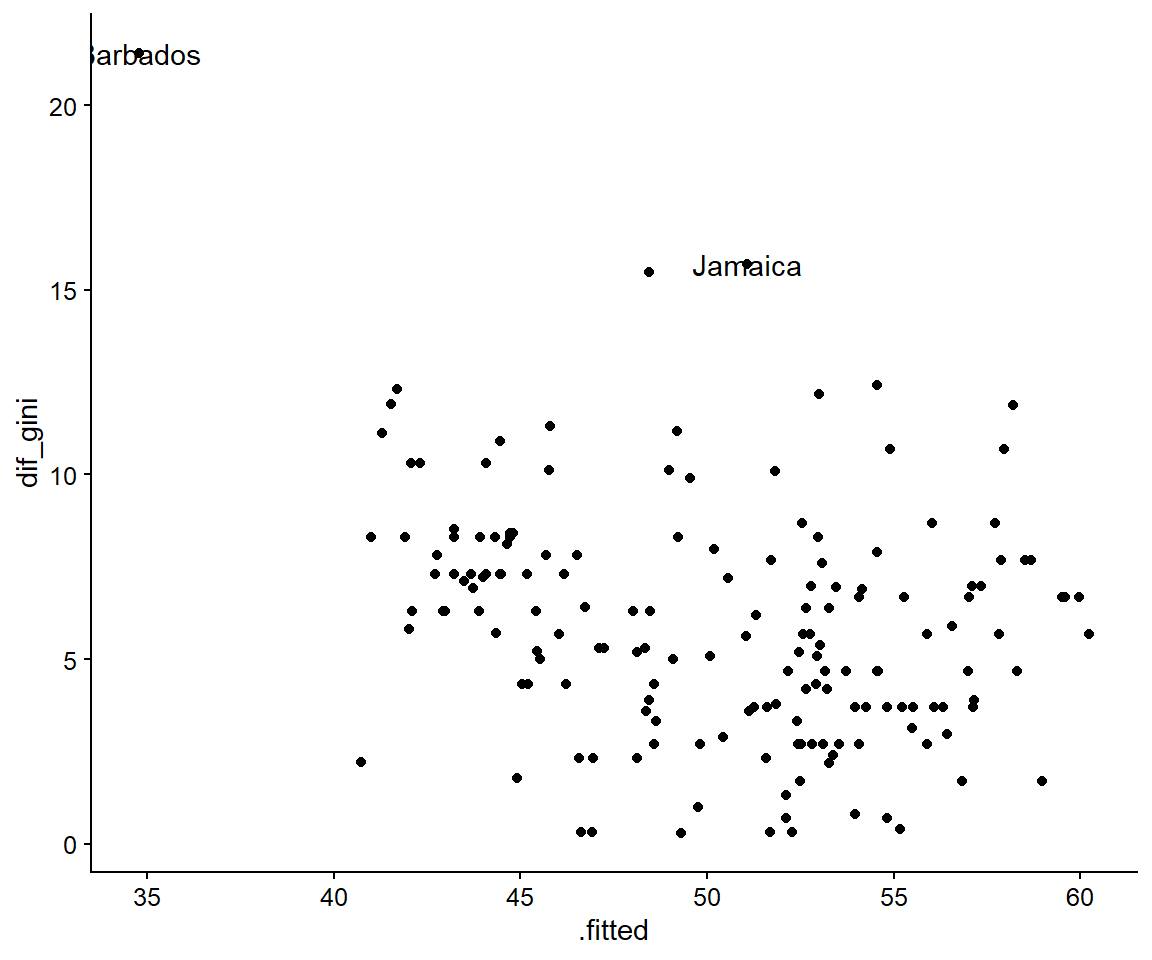

Figura 3.11: Los dos casos extremos más importantes según el índice de Gini

Una vez más, Barbados y Jamaica aparecen como casos atípicos en la variable dependiente. Ambos tienen en común que fueron colonias caribeñas del Imperio Británico. ¿Tal vez, podríamos incluir este control para todos los países con este legado y ver cómo se ajusta al nuevo modelo? Si aparecen grandes cambios en los valores previstos, podríamos explorar con pruebas cualitativas el papel que tuvieron las instituciones coloniales del Imperio Británico sobre la desigualdad de estas colonias.

6.2.5 Casos más similares

La selección de casos similares implica la identificación de dos casos que sean similares. Si estamos en la etapa exploratoria de nuestro proyecto de investigación y no tenemos fuertes supuestos teóricos (aún no hemos identificado una variable independiente clave en particular), buscamos un par de observaciones que sean más similares en las variables independientes pero que difieran en la variable dependiente. De esta manera, el objetivo será identificar uno o más factores que difieren entre los casos y que pueden explicar la divergencia del resultado. Esta estrategia es la del método directo de acuerdo de Stuart Mill.

Sin embargo, cuando ya tenemos una teoría sobre cómo una variable independiente afecta a la variable dependiente, la selección de casos consiste en identificar dos casos que son similares en todas las covariables pero que difieren en la variable independiente de interés. En este caso, el enfoque será confirmar el argumento y explorar más a fondo los mecanismos causales que conectan la variable independiente con la dependiente.

Para seleccionar casos similares, se recomienda utilizar una técnica de matching (Gerring 2006, 134). En palabras sencillas, esta técnica consiste en emparejar pares de observaciones que sean lo más similares posible en todas las covariables, pero que difieran en la variable independiente de interés. Para simplificar el análisis, estas variables independientes tienden a ser dicotómicas, emulando un escenario experimental en el que hay un tratamiento (1) y un placebo o control (0). De esta manera, el objetivo es hacer coincidir pares en los que una observación pertenece al grupo de tratamiento y la otra al grupo de control.

Dado que fundar pares que coincidan en todas las covariables puede ser bastante difícil de lograr, se utiliza a menudo un procedimiento de emparejamiento basado en las puntuaciones de propensión. Este procedimiento consiste en fundar pares de observaciones que tienen probabilidades estimadas similares de estar en el grupo de tratamiento (con un valor de 1 en la variable independiente de interés), condicionadas por las variables de control. Para aplicar este método de selección de casos en nuestra investigación, crearemos una variable de tratamiento ficticia (para la variable de gasto en educación), en la que 0 es un gasto menor o igual a la media de la muestra y 1 si el gasto es mayor que la media.

bienestar_sinna <- bienestar_sinna %>% 
  mutate(treatment = if_else(gasto_educ > mean(gasto_educ), 1, 0))

Ahora que tenemos una variable de tratamiento, podemos estimar las puntuaciones de propensión. Es decir, la probabilidad de estar en el grupo de tratamiento (gasto en educación mayor que la media de la muestra) condicionada por las variables de control del modelo. Esta estimación se hace en base a un modelo Logit, ya que nuestras variables dependientes son una variable dicotómica.

m_propensityscore <- glm(treatment ~ dualismo_sectorial + inversion_extranjera + pib +
                           poblacion + diversidad_etnica + tipo_regimen + 
                           tipo_regimen * gasto_segsocial + gasto_salud + gasto_segsocial +
                           bal_legislativo + represion, 
                         data      = bienestar_sinna, 
                         family    = binomial(link = logit), 
                         na.action = na.exclude)

Como hicimos con el modelo general de los determinantes de la desigualdad, crearemos una base de datos con el comando augment para guardar algunas estadísticas que serán útiles para seleccionar los casos.

propensity_scores<- augment(m_propensityscore, data = bienestar_sinna,
                            type.predict = "response") %>%
  dplyr::select(propensity_scores = .fitted, pais, treatment, anio,
                gini)

Ahora, identificamos los casos con las puntuaciones de propensión más bajas tanto para el grupo de tratamiento (alto gasto en educación) como para el grupo de control (bajo gasto en educación) para decidir la selección de los casos. Cabe señalar que esto también puede hacerse para las puntuaciones de propensión altas: lo importante es que deben tener puntuaciones similares o “cercanas” (igual probabilidad de recibir tratamiento). Veamos los casos con puntuaciones de propensión bajas, en el grupo de países con gastos superiores a la media de la muestra:

propensity_scores %>%
  filter(treatment == 1) %>%
  arrange(propensity_scores) %>%
  dplyr::select(pais, anio, propensity_scores) %>%
  slice(1:2)
## # A tibble: 2 x 3
##   pais    anio propensity_scores
##   <chr>  <dbl>             <dbl>
## 1 Brasil  1984            0.0815
## 2 México  2000            0.159

Por otra parte, observemos los casos con una baja puntuación de propensión entre los países con un gasto en educación inferior al promedio de la muestra:

propensity_scores %>%
  filter(treatment== 0) %>%
  arrange(propensity_scores) %>%
  dplyr::select(pais, anio, propensity_scores) %>%
  slice(1:2)
## # A tibble: 2 x 3
##   pais       anio propensity_scores
##   <chr>     <dbl>             <dbl>
## 1 Paraguay   1994           0.00309
## 2 Argentina  1982           0.00673

De acuerdo con los resultados, tanto Brasil como México podrían ser seleccionados para ser comparados con Paraguay o Argentina para llevar a cabo estudios de casos más exhaustivos y similares. Teniendo en cuenta su proximidad geográfica, podríamos comparar Brasil con Argentina, e intentar explicar de qué manera el gasto en educación ha impactado en la equidad de los ingresos en ambos países.

Ejercicio 6B. Seleccione pares de casos más similares tomando la Inversión Extranjera Directa inversion_extranjera como una variable independiente (tratamiento).

6.2.6 Casos mas diferentes

El procedimiento para seleccionar los casos más diferentes implica una lógica opuesta a la de los casos más similares. Aquí buscamos observaciones que son diferentes en las variables de control, pero similares en el valor asumido por la variable independiente y la variable dependiente. En resumen, lo que buscamos son diferentes puntuaciones de propensión pero similares en la variable independiente y en la dependiente.

Cabe señalar que este tipo de selección de casos es útil cuando se supone una “causa única” (Gerring 2006, pág. 143). Es decir, cuando la variación de la variable dependiente es causada por una sola variable (o cuando nos interesa explicar el efecto de un solo factor). Si lo que interesa es indagar sobre la combinación de diferentes factores causales, este procedimiento de selección de casos no es el más adecuado. Para seleccionar los casos “más diferentes,” también utilizaremos las puntuaciones de propensión, pero ahora estamos interesados en seleccionar pares con resultados iguales en la variable dependiente, así como en la variable independiente, y con puntuaciones de propensión muy diferentes.

Veamos, entonces, cuáles son estos casos. Primero, creamos una variable ficticia para un Gini por encima o por debajo de la media. Luego, identificamos los casos tratados con bajas puntuaciones de propensión (baja probabilidad de tener un gasto por encima de la media) que tienen valores de Gini mayores que la media de la muestra (gini == 1) y valores de gasto en educación menores que la media de la muestra (treatment == 0):

propensity_scores <- propensity_scores %>% 
  mutate(gini = if_else(gini > mean(gini, na.rm = T), 1, 0))

propensity_scores %>%
  filter(gini == 1 & treatment == 0) %>%
  arrange(propensity_scores) %>%
  dplyr::select(pais, anio, propensity_scores) %>%
  slice(1:2)
## # A tibble: 2 x 3
##   pais      anio propensity_scores
##   <chr>    <dbl>             <dbl>
## 1 Paraguay  1999           0.00953
## 2 Paraguay  1997           0.0221

A continuación, repetimos el mismo proceso para las puntuaciones de propensión más altas (es decir, cuando la probabilidad de recibir tratamiento - tener un gasto en educación mayor que la media - es muy alta). En otras palabras, identificamos los casos con la puntuación de propensión más alta para valores de Gini mayores que la media de la muestra (gini == 1) y gastos en educación menores que la media de la muestra (treatment == 0):

propensity_scores %>%
  filter(gini == 1 & treatment == 0) %>%
  arrange(-propensity_scores) %>%
  dplyr::select(pais, anio, propensity_scores) %>%
  slice(1:2)
## # A tibble: 2 x 3
##   pais      anio propensity_scores
##   <chr>    <dbl>             <dbl>
## 1 Honduras  1994             0.983
## 2 Honduras  1996             0.969

Nuestros resultados sugieren que Paraguay podría ser seleccionado para ser comparado con Honduras para llevar a cabo un estudio de caso “muy diferente.” Ambos tienen un bajo gasto en educación como porcentaje de su PIB, y ambos son muy desiguales, aunque son muy diferentes en las variables de control.

6.3 La importancia de la combinación de métodos

Para concluir, consideramos importante insistir en la pertinencia de la combinación de métodos para responder a una pregunta de investigación. Aunque los métodos apropiados dependerán de la pregunta de investigación, la respuesta a un fenómeno requiere tanto la identificación de una relación entre dos (o más) variables como una explicación detallada sobre la forma en que esas dos variables se vinculan entre sí y por qué se produce el efecto indicado. Para abordar estas dos dimensiones es necesario combinar diferentes estrategias empíricas, a fin de explotar las respectivas virtudes y complementar sus debilidades.

Una estimación a través de MCO nos permite identificar las relaciones promedio entre dos variables en un gran número de observaciones, algo que la investigación cualitativa no puede realizar. Sin embargo, MCO no puede responder por qué o cómo se producen estas relaciones y, para ello, es necesario un diseño de investigación cualitativa que profundice en los procesos y agentes que “explican” estas relaciones. Por supuesto, el proceso también puede realizarse al revés: primero, podríamos identificar una relación entre dos variables a partir de un estudio de caso en profundidad, y luego, probar esta relación en otros casos a través de un estudio cuantitativo de n-grande para evaluar la generalización del descubrimiento. En cualquier caso, se recomienda la combinación de métodos para ofrecer explicaciones más complejas y completas sobre los fenómenos que nos interesa estudiar.

Ejercicio 6C. - Estime de un modelo donde la variable dependiente es la puntuación de Gini (gini) y el gasto en educación de los independientes (gasto_educ), gasto en salud (gasto_salud), gasto en seguridad social (gasto_segsocial), PIB (pib), e inversión extranjera directa (inversion_extranjera). - Seleccione los casos típicos, atípicos e influyentes para este modelo. ¿Qué variables pueden ser importantes para entender los valores atípicos? - Ahora, supongamos que su variable de interés independiente es la Inversión Extranjera Directa. Seleccione los casos extremos en x, los casos extremos en y, los casos más similares y más diferentes.

E-mail: ifynn@uc.cl ↩︎
E-mail: lnocetto@uc.cl ↩︎
Es posible que con buenas variables instrumentales, pero no las cubrimos en este libro↩︎
Un gran ejemplo de rastreo de procesos aplicado a la ciencia política latinoamericana es el libro de Pérez, Piñeiro y Rosenblatt en el caso del activismo partidario en Uruguay (https://www.cambridge.org/core/books/how-party-activism-survives/93C5584DB63DF0A80B51F3EEB68BC8E9)↩︎
si ya te estás preguntando qué ocurrió en Jamaica, te recomendamos este artículo: Handa, S., & King, D. (1997). Structural adjustment policies, income distribution and poverty: a review of the Jamaican experience. World Development, 25(6), 915-930.↩︎