Capítulo 15 Análisis de componentes principales
Caterina Labrín60 y Francisco Urdinez61
Lecturas sugeridas
Abeyasekera, S. (2005). Multivariate methods for index construction. In Household Sample Surveys in Developing and Transition Countries, pages 367–387. United Nations, New York, NY.
Bryant, F. B. (2000). Assessing the Validity of Measurement. In Grimm, L. G. and Yarnold, P. R., editors, Reading and Understanding MORE Multivariate Statistics, pages 99–146. American Psychological Association, Washington, DC.
Collier, D., Laporte, J., and Seawright, J. (2008). Typologies: Forming concepts and creating categorical variables. In Box-Steffensmeier, J. M., Brady, H. E., and Collier, D., editors, The Oxford Handbook of Political Methodology, pages 152–173. Oxford University Press, Oxford.
Goertz, G. (2006). Social Science Concepts: A User’s Guide. Princeton University Press, Princeton, NJ.
- Capítulo 4 - “Increasing Concept-Measure Consistency.”
Jackman, S. (2008). Measurement. In Box-Steffensmeier, J. M., Brady, H. E., and Collier, D., editors, The Oxford Handbook of Political Methodology, pages 119–151. Oxford University Press, Oxford.
Los paquetes que necesitas instalar
tidyverse(Wickham 2019b),paqueteadp(Urdinez and Cruz 2020),FactoMineR(Husson et al. 2020),factoextra(Kassambara and Mundt 2020),GGally(Schloerke et al. 2020),ggcorrplot(Kassambara 2019).
15.1 Introducción
A estas alturas del libro has aprendido muchas herramientas para trabajar bien con los datos y conceptos de las ciencias sociales. En este capítulo verás cómo crear de forma sencilla variables que midan conceptos complejos que muchas veces en las ciencias sociales, y especialmente en las ciencias políticas, queremos utilizar para probar hipótesis o simplemente visualizar cómo se comportan.
La relación entre guerra y democracia o entre democracia y desarrollo económico son cosas que se suelen estudiar en las ciencias políticas. Sin embargo, estos conceptos a veces no están claramente definidos de antemano o si lo están, no sabemos cuál de las definiciones puede servirnos. Conceptos como terrorismo o populismo son utilizados a diario por políticos y periodistas, muchas veces de forma incorrecta, demostrando que el problema no sólo se da a nivel académico sino en toda la sociedad, generando niveles de desinformación bastante graves. Esta fragilidad de nuestros conceptos se hace aún más grave si tenemos que operar con datos, ya que muchas veces queremos medir conceptos complejos con indicadores que nos muestren las variaciones o relaciones con otros conceptos de una manera más cuantitativa o visual.
Para ilustrar la situación, tomemos un caso hipotético: pretendamos que estamos trabajando en un proyecto que entre otras cosas pide comparar cómo se comportan los países democráticos de América Latina y por lo tanto debe ser capaz de visualizarlo claramente en una tabla o gráfico. Normalmente, en este caso, buscaríamos algún indicador de la democracia que V-dem o Freedom House nos da para todos los países de América Latina. Asumiríamos por la práctica que estos indicadores tienen una validez evidente y que fueron construidos adecuadamente, basadas en dimensiones claras. Nadie cuestionaría nuestra elección. Ahora, imaginemos que queremos investigar un concepto diferente y más específico. Para esta tarea no tenemos un indicador similar a los de la democracia y debemos empezar de cero: ¿qué estamos midiendo? ¿cómo lo medimos? ¿Qué datos utilizamos?
Ante este problema, en este capítulo queremos ilustrar la utilidad del Análisis de Componentes Principales (ACP) ya que nos permite generar las diferentes dimensiones que conforman un concepto abstracto a través de la reducción de diferentes indicadores previamente elegidos. Esto es principalmente para analizar cómo se compondría un concepto de este estilo y para entender lo que estamos explorando. Además, presentaremos algunas formas de operativizar los conceptos a través de índices que nos pueden mostrar la variabilidad de la medición entre las diferentes unidades de análisis, para poder compararlos o incluirlos dentro de un análisis más complejo.
15.1.1 Conceptos, medidas y validez
Cuando construimos una medición empírica a partir de un concepto abstracto (como son democracia, populismo, desarrollo), además de tener en cuenta su complejidad, queremos que sea válida (ver Grimm and Yarnold 2000 para un excelente resumen sobre los diferentes tipos de validez). La validez del contenido es la que nos permite asegurar que la medición corresponde a lo que está definido conceptualmente para esa medición. Esto debe garantizarse cada vez que queramos generar un concepto a través de una revisión teórica que determine adónde irá nuestro concepto, cuáles serán las partes que lo compondrán y principalmente qué variables utilizaremos para medirlas. Una adecuada revisión de la literatura sobre el concepto concreto en el que estamos trabajando, que pueda situarse en un marco teórico más amplio, siempre será más que deseable cuando se trabaje con conceptos abstractos y complejos.
La validez de la construcción se refiere a la propiedad de un concepto que mide lo que dice medir. Esta validez siempre debe ser cuestionada, precisamente por lo que dijimos anteriormente sobre la complejidad de los conceptos con los que trabajamos. Por ejemplo, es muy frecuente con las medidas que existen de la democracia. Incluso cuando hemos avanzado enormemente como disciplina y tenemos mediciones comparables entre países y a lo largo del tiempo, como en el caso Polity IV y V-Dem, existen diferentes opiniones sobre cómo debe ser operativizado este concepto y siempre hay espacio para mejoras.
Hay dos maneras de ganar validez de construcción para nuestra variable de interés. La primera alternativa para obtener la validez de constructo se llama validez discriminatoria, es decir, nuestro constructo no debe estar altamente correlacionado con variables que nuestro indicador no pretende medir. Este concepto puede ejemplificarse muy bien con la forma en que V-Dem ha elegido para crear su índice de democracia (al que llaman poliarquía): como su nombre indica, miden variedades de democracia de diferentes dimensiones, a saber, las dimensiones liberal, participativa, deliberativa, electoral e igualitaria. Cabe esperar que las dimensiones no estén muy correlacionadas entre sí para tener la seguridad de que captan realmente las diferentes caras de este concepto polifacético.
La segunda alternativa es la de la validez convergente, es decir, la correlación de mi medida de interés con las medidas de los demás. Por ejemplo, la democracia medida por V-Dem tiene una correlación de 0,8 con la forma en que es medida por Polity IV. Si creo una tercera medida, cuya correlación es 0,70 con Polity y 0,9 con V-Dem, puedo estar seguro de que las tres variables son similares a la variable latente.
La técnica de Análisis de Componentes Principales (PCA, por sus siglas en inglés) nos ayuda a definir qué combinación de datos representa mejor el concepto que queremos medir.
15.2 Cómo funciona el Análisis de Componentes Principales
La ACP (o PCA) es una técnica muy útil cuando queremos trabajar con diferentes variables con un solo concepto. Al elegir previamente las variables con las que queremos trabajar, la técnica PCA nos da diferentes componentes, que son la reducción de la dimensionalidad de una base de datos multivariante que condensan las dimensiones en una sola variable. Consiste literalmente en trabajar con la correlación entre las variables, y dar cuenta de lo que miden en común y lo que cada una mide individualmente.
El PCA aglutina las correlaciones entre las variables y las condenas en un solo componente. Cuanto más parecidas sean las variables (altas correlaciones y en la misma dirección) menos componentes se necesitarán para captar toda la complejidad de los datos.
La PCA nos dará un número de “componentes” igual al número de variables. Sin embargo, no necesitaremos todos ellos para condensar las variables y sólo conservaremos unos pocos. Ayuda pensar en PCA como un batido, las variables que ejecutamos son como la fruta que ponemos en la licuadora, mientras que los componentes son los sabores que obtenemos de la mezcla. Por ejemplo, si hacemos funcionar PCA con cuatro variables (X, Y, W, Z) obtenemos cuatro componentes (siempre obtenemos el mismo número de componentes que de variables). Suponga que obtenemos que el componente 1 está alta y positivamente correlacionado con las variables X y W, el componente 2 está alta y negativamente correlacionado con Y y W, el componente 3 está alta y positivamente correlacionado con la variable Z y débilmente y negativamente correlacionado con X, y el componente 4 está débilmente y positivamente correlacionado con Y y W. Del análisis sabemos que si mantenemos los componentes 1 y 2 nuestro índice será lo suficientemente bueno. ¿Cómo decidimos cuál y cuantos mantenemos?
Los componentes vendrán con un Eigenvalor, que es un puntaje que mide cuánta varianza de las variables originales explica cada componente. El Eigenvalor ordena los componentes de mayor a menor varianza explicada. Como regla general, mantenemos los componentes cuyos Eigenvalor sean mayores que 1.
La creación de diferentes componentes debido al PCA le será útil para crear índices. Ahora daremos un ejemplo en R.
15.3 Nociones básicas en R
En América Latina, dado el pasado de gobiernos dictatoriales y el reciente debilitamiento democrático de muchos países, puede ser importante para una posible investigación considerar la opinión pública sobre las instituciones de los países. Una buena pregunta que se puede hacer es ¿cómo se puede saber cuál es la opinión de los ciudadanos latinoamericanos sobre las instituciones democráticas de sus países?
El Proyecto de Opinión Pública Latinoamericana (LAPOP por sus siglas en inglés) - coordinado desde la Universidad de Vanderbilt - se especializa en la realización de estudios de evaluación de impacto y en la producción de informes sobre las actitudes, evaluaciones y experiencias de los individuos en los países de América Latina. Este proyecto proporciona a los investigadores diferentes preguntas que, en conjunto, podrían ayudarnos a aproximar el grado de confianza que existe en la región respecto de las instituciones democráticas del país correspondiente a cada individuo.
Ejercicio 15A. Asumamos que se te pide que midas el antiamericanismo en América Latina. ¿Cómo medirías este concepto? Elige 5 o más preguntas de la encuesta LAPOP (puedes consultar el libro de códigos aquí) que usarías para medir el antiamericanismo.
Como primer paso, es importante seleccionar las variables que se utilizarán para llevar a cabo el LAPOP, dejando de lado todo lo que no queremos utilizar en el índice final. Estos datos contienen doce preguntas de la encuesta LAPOP, realizada a una muestra de alrededor de 7000 personas en 10 países de América Latina. Se puede acceder al cuestionario completo en este link. Este primer paso es esencial. Es el paso que implica más trabajo teórico para el investigador, ya que a partir de aquí se definen las variables que se integrarán en el análisis (y que se dejarán fuera). En nuestro análisis, las variables que usamos son las siguientes:
| Nombre | Descripción | Fuente |
|---|---|---|
| justifica_golpe | Variable dicotómica que mide el nivel de justificación de los golpes de estado militares en el país del encuestado contra un gran número de delitos. | Basada en la pregunta “jc10” de la encuesta del LAPOP. |
| justifica_cierre_cong | Variable dicotómica que mide el nivel de justificación del cierre del congreso en situaciones difíciles por el presidente. | Basada en la pregunta “jc15a” de la encuesta del LAPOP. |
| conf_cortes | Mide en una escala del 1 al 7 el nivel de confianza en los tribunales en el país del encuestado. | Encuesta LAPOP. |
| conf_instit | Mide en una escala del 1 al 7 el nivel de respeto a las instituciones políticas en el país del encuestado. | Encuesta LAPOP. |
| conf_congreso | Mide en una escala de 1 a 7 el nivel de confianza en el Congreso Nacional (poder legislativo) del país del encuestado. | Encuesta LAPOP. |
| conf_presidente | Mide en una escala de 1 a 7 el nivel de confianza en el presidente (poder ejecutivo) del país del encuestado | Basado en la pregunta “b21a” de la escuesta LAPOP. |
| conf_partidos | Mide en una escala de 1 a 7 el nivel de confianza en los partidos políticos del país del encuestado | Basado en la pregunta “b21a” de la escuesta LAPOP. |
| conf_medios | Mide en una escala del 1 al 7 el nivel de confianza en los medios de comunicación en el país del encuestado | Basado en la pregunta “b37” de la encuesta LAPOP. |
| conf_elecciones | Mide en una escala del 1 al 7 el nivel de confianza en las elecciones del país del encuestado. | |
| satisfecho_dem | Variable dicotómica que mide el nivel de satisfacción con la democracia de los encuestados. Basada en la pregunta “pn4” de la encuesta LAPOP. | |
| dervote | Mide en una escala del 1 al 7 la satisfacción con la idea de que aquellos que están en contra del gobierno en el poder pueden votar en las elecciones del país del encuestado | Basada en la pregunta “d1” de la encuesta LAPOP. |
| manifestaciones | Mide en una escala del 1 al 7 la satisfacción con la idea de que aquellos que están en contra del gobierno en el poder pueden llevar a cabo manifestaciones pacíficas para expresar su punto de vista | Basada en la pregunta “d2” de la encuesta LAPOP. |
Para poder seleccionar las variables y usar los pipes (%>% ) cargamos ‘tidyverse.’ Luego, cargamos la base de datos del paquete del libro, paqueteadp.
library(tidyverse)library(paqueteadp)
data("lapop")lapop
## # A tibble: 7,655 x 14
## id pais_nombre justifica_golpe justifica_cierr~ conf_cortes
## <dbl> <chr> <dbl> <dbl> <dbl>
## 1 1 Argentina 0 1 6
## 2 2 Argentina 1 0 4
## 3 3 Argentina 0 0 4
## # ... with 7,652 more rows, and 9 more variablesEstas variables pueden ser exploradas gráficamente. Por ejemplo, podemos ver -por país- la confianza que tienen sus ciudadanos en las elecciones:
lapop <- lapop %>%
group_by(pais_nombre) %>%
mutate(conf_elecciones_prom = mean(conf_elecciones)) %>%
ungroup()
ggplot(lapop, aes(x = conf_elecciones)) +
geom_histogram() +
labs(title = " Confianza en las elecciones ",
x = " En azul, el promedio nacional ", y = "conteo")+
facet_wrap(~pais_nombre) +
geom_vline(aes(xintercept = conf_elecciones_prom),
color = "blue", linetype = "dashed", size = 1)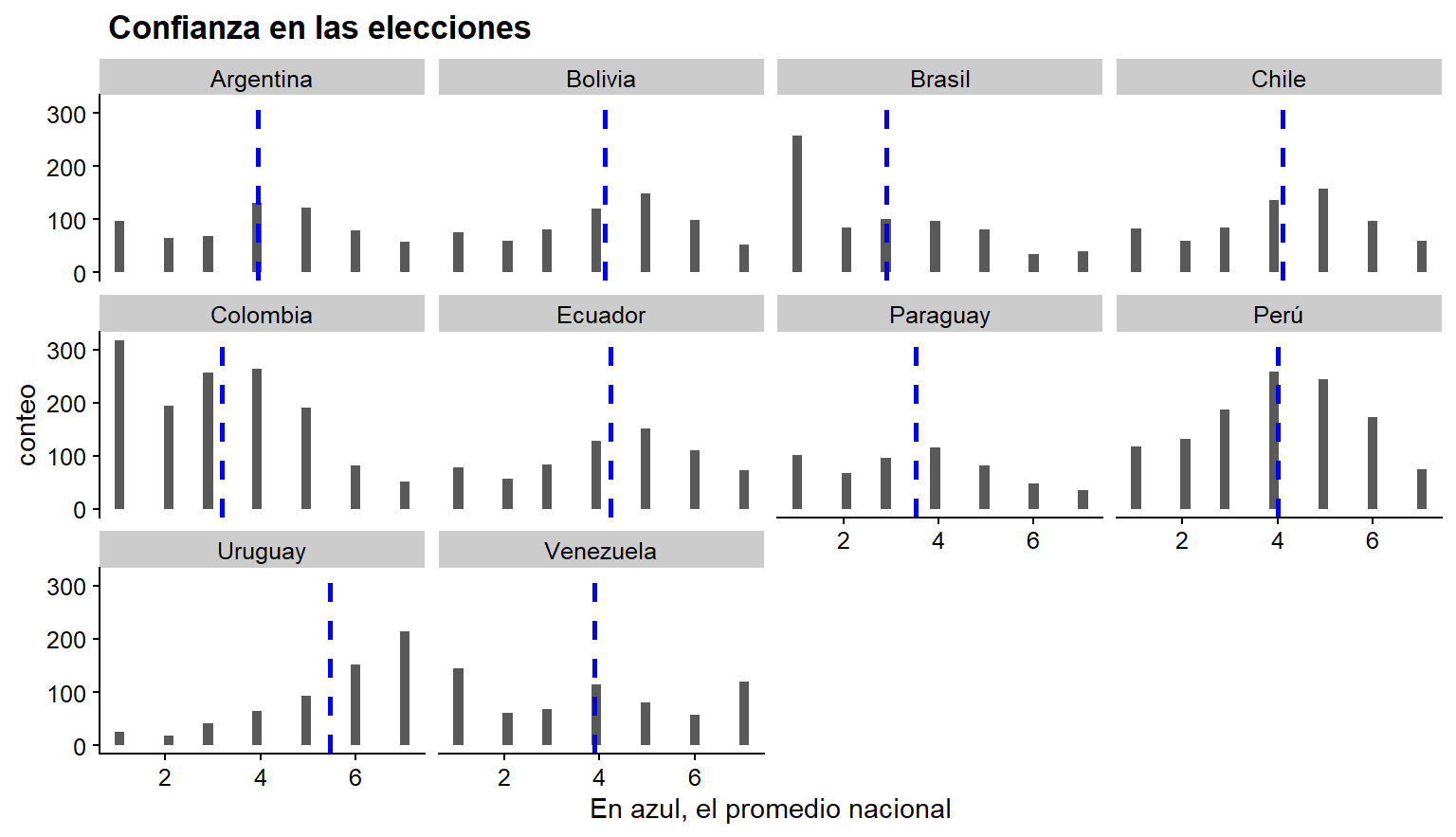
Figura 3.3: Histogramas de confianza en las elecciones por país. En azul, los promedios nacionales
Seleccionemos nuestras variables de interés, esto significa que dejamos fuera cualquier variable que no sea representativa de la democracia, por ejemplo la variable ‘pais’ que indica el país de cada individuo no debe ser incorporada. Para ello, generamos una nueva base de datos que contiene sólo las variables que queremos utilizar, en este caso, para saber cuál es la opinión que los latinoamericanos tienen de sus instituciones democráticas.
lapop_num <- lapop %>%
select(justifica_golpe, justifica_cierre_cong, conf_cortes, conf_instit, conf_congreso, conf_presidente, conf_partidos, conf_medios,
conf_elecciones, satisfecho_dem, voto_opositor, manifestaciones) %>%
mutate_all(as.numeric)
lapop
## # A tibble: 7,655 x 15
## id pais_nombre justifica_golpe justifica_cierr~ conf_cortes
## <dbl> <chr> <dbl> <dbl> <dbl>
## 1 1 Argentina 0 1 6
## 2 2 Argentina 1 0 4
## 3 3 Argentina 0 0 4
## # ... with 7,652 more rows, and 10 more variablesHabiendo ya seleccionado las variables, el primer paso es estandarizarlas. La técnica PCA acepta variables de diferentes tipos, pero es importante omitir o imputar a los promedios los valores perdidos. En este caso, omitiremos los posibles NA que tenga la base de datos.
lapop_num <- lapop_num %>%
scale() %>%
na.omit() %>%
as_tibble()El siguiente paso es observar la correlación entre variables. Esto es útil para saber cómo se relacionan las variables elegidas, y también para ver si hay correlaciones extremadamente altas entre dos o más variables. Si se da el caso de que tenemos dos o más variables con alta correlación entre ellas, éstas tendrán una enorme influencia en la orientación de los componentes.
La mejor alternativa para observar la correlación entre las variables es la que ofrece el paquete GGally. Cuanto más intenso es el color, más fuerte es la correlación. En el azul tendremos correlaciones negativas, y en el rojo correlaciones positivas.
library(ggcorrplot)
corr_lapop <- lapop_num %>%
# calculate correlation matrix and round to 1 decimal place:
cor(use = "pairwise") %>%
round(1)
ggcorrplot(corr_lapop, type = "lower", lab = T, show.legend = F)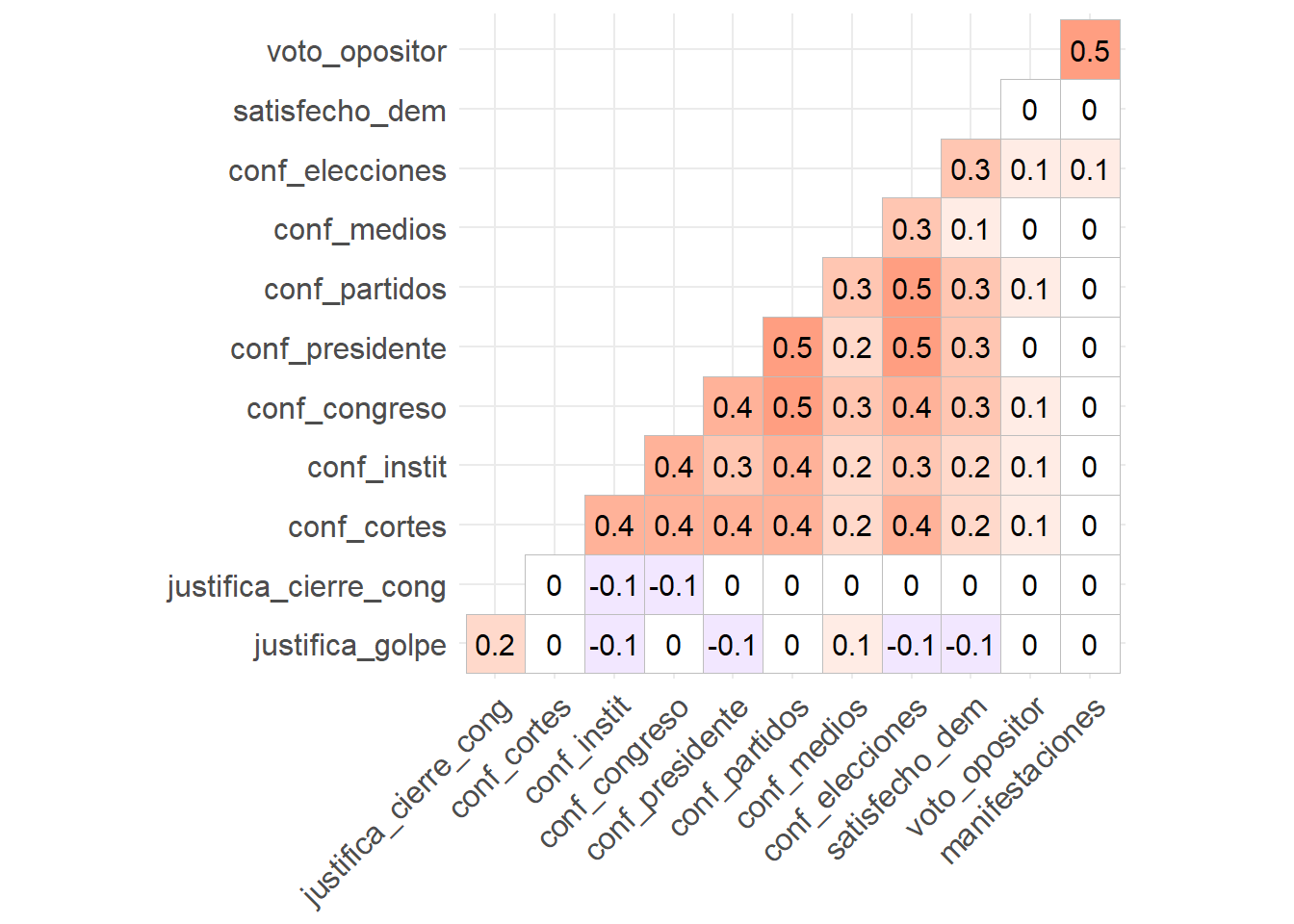
Figura 3.6: Matriz de correlación de las variables que usaremos en nuestro análisis
Lo que vemos es que las variables de confianza están positivamente correlacionadas. Es decir, los que confían en el presidente tienden a confiar en los medios de comunicación, las elecciones, por ejemplo.
Una vez que vemos las correlaciones, estamos listos para hacer el PCA. Para ello, utilizaremos dos paquetes diferentes que realizan el PCA, esto para proporcionar opciones de cómo realizar la técnica en R. El PCA nos permitirá definir a través de los componentes cuáles serán las dimensiones del concepto que guardamos, para luego avanzar a realizar un índice simple que denote la variación del concepto a través de diferentes unidades de análisis.
15.4 Dimensionalidad del concepto
Primero, con el subconjunto de datos, generamos un PCA con el paquete de stats, que es uno de los paquetes básicos de R (ya viene instalado). Luego con el comando summary() podemos ver lo que el análisis nos da.
pca <- princomp(lapop_num)
summary(pca, loadings = T, cutoff = 0.3)
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## Standard deviation 1.86 1.22 1.11 0.976 0.893 0.882 0.827
## Comp.8 Comp.9 Comp.10 Comp.11 Comp.12
## Standard deviation 0.800 0.750 0.725 0.686 0.657
## [ reached getOption("max.print") -- omitted 2 rows ]
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## justifica_golpe 0.693 0.501
## Comp.8 Comp.9 Comp.10 Comp.11 Comp.12
## justifica_golpe 0.304
## [ reached getOption("max.print") -- omitted 11 rows ]Como puedes ver, hay tres componentes que nos dan un Eigenvalor (denotado por la desviación estándar) mayor que 1. Este límite será nuestro criterio para seleccionar los componentes que mantendremos. También nos muestra cómo se construye cada componente con las variables que seleccionamos.
Otra forma de ver los Eigenvalores de cada componente es con el comando get_eigenvalue() del paquete factoextra. Como obtuvimos con summary(), get_eigenvalue nos da además del Eigenvalor, la varianza combinada que cada componente explica.
library(factoextra)
eig_val <- get_eigenvalue(pca)
eig_val
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 3.44 28.7 29
## Dim.2 1.48 12.3 41
## Dim.3 1.23 10.3 51
## Dim.4 0.95 7.9 59
## Dim.5 0.80 6.6 66
## Dim.6 0.78 6.5 72
## [ reached 'max' / getOption("max.print") -- omitted 6 rows ]Como puede verse, el componente 1 representa alrededor del 28,7% de la varianza total de las variables elegidas. La varianza de los otros dos componentes importantes es del 12,3% y del 10,3% respectivamente.
Otra forma de entregar esta información es a través de gráficos. El siguiente comando nos da en su forma más simple, el porcentaje de varianza explicada por cada uno de los componentes que el PCA nos da.
fviz_eig(pca, addlabels = T, ylim = c(0, 50))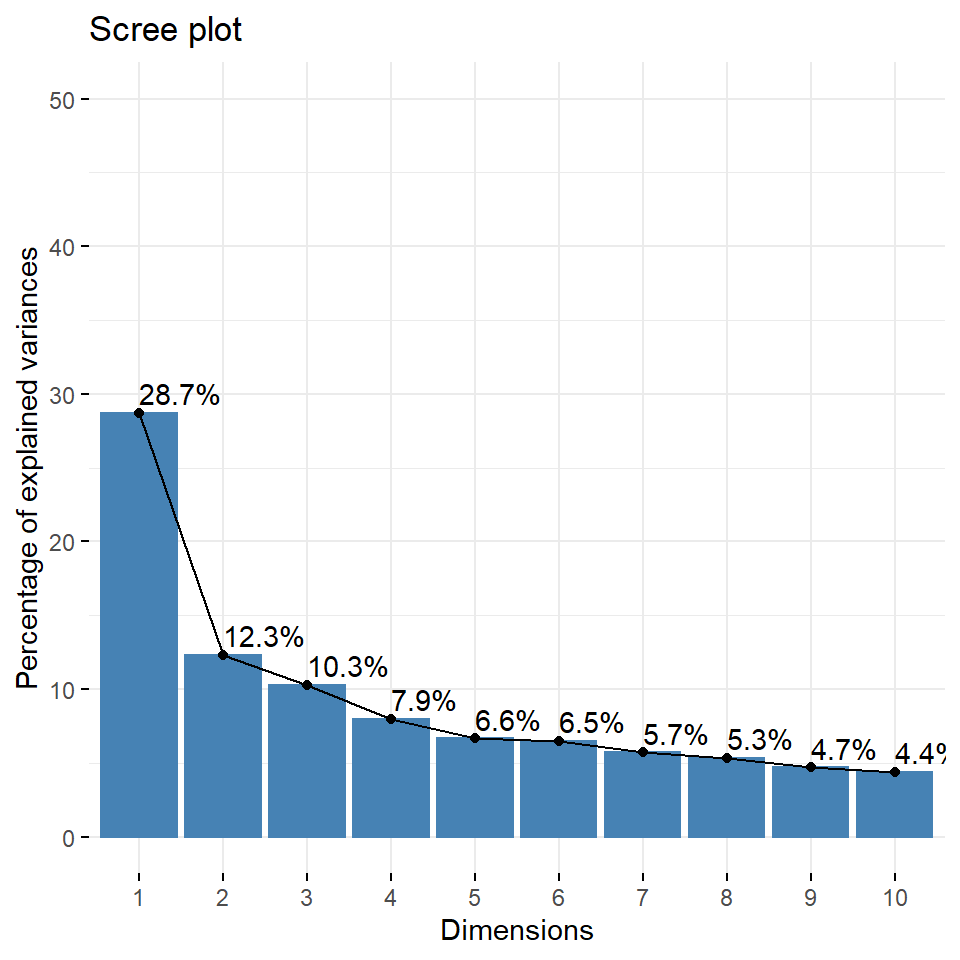
Figura 3.9: Porcentaje de la varianza explicada de cada componente
Un pequeño cambio en el comando, también nos da un gráfico con los valores propios de cada uno de los componentes:
fviz_eig(pca, choice = c("eigenvalue"), addlabels = T, ylim = c(0, 3))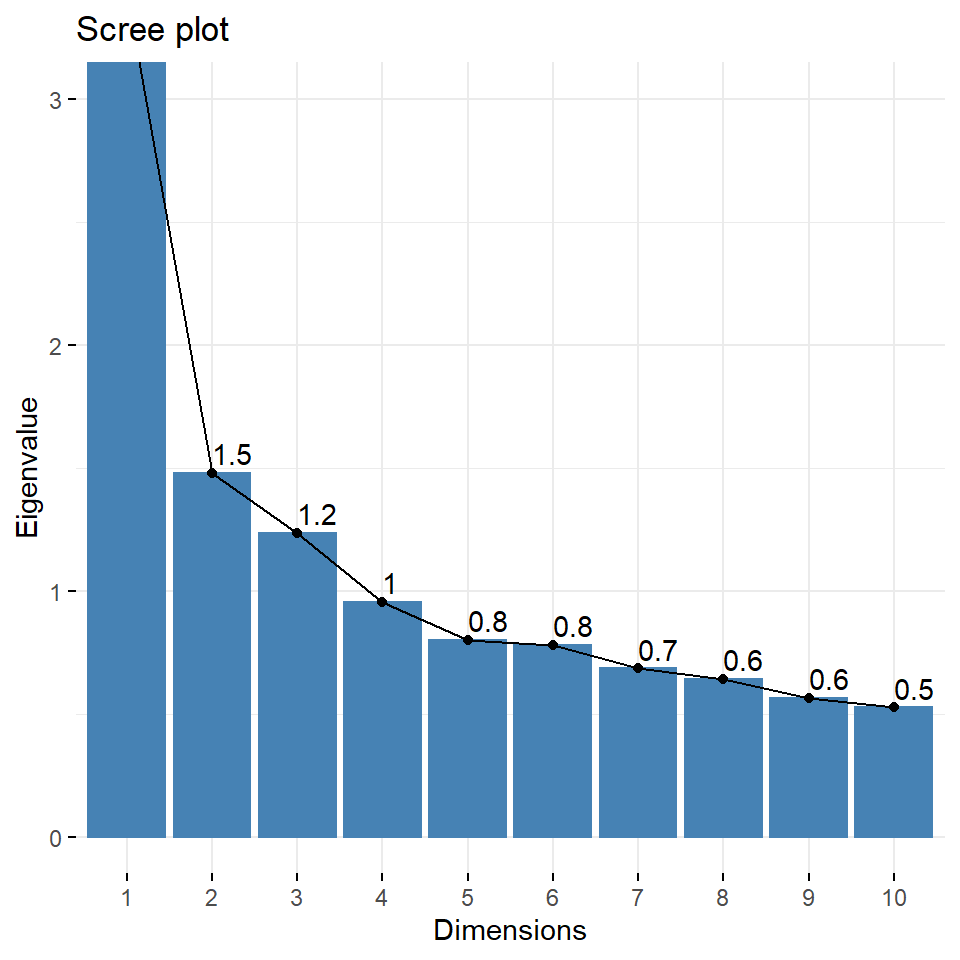
Figura 3.10: Eigenvalor de cada componente
Para saber cómo está compuesto cada uno de estos componentes, podemos generar un Biplot. Este tipo de gráfico nos aparecerá como vectores en dos dimensiones (que serán los dos primeros componentes del análisis).
fviz_pca_biplot(pca, repel = F, col.var = "black", col.ind = "gray")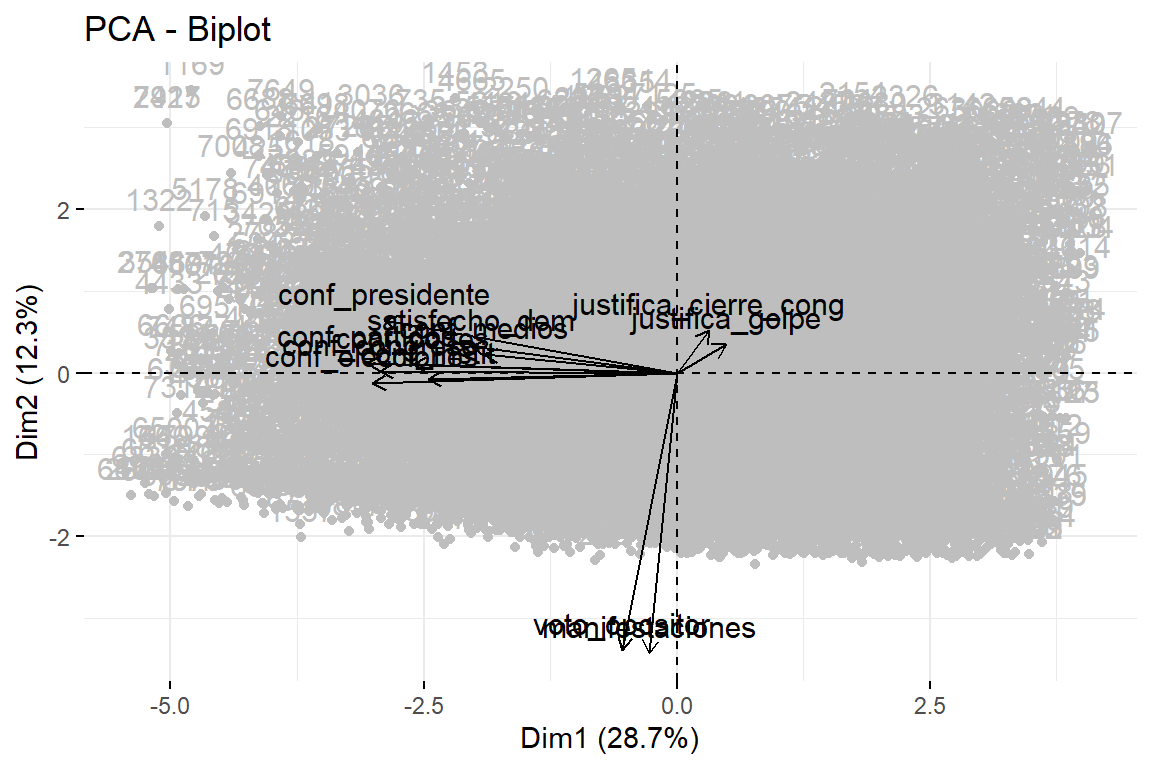
Figura 3.11: Biplot con las dimensiones 1 y 2
Este gráfico bidimensional muestra claramente que tenemos tres grupos de variables. Estos conjuntos de variables son los que se reducen precisamente a tres componentes, que pueden representar tres dimensiones de opinión sobre las instituciones políticas que queremos medir en América Latina.
También podemos saber, cómo se compondrán las dimensiones del concepto que queremos medir con el comando fviz_contrib, cambiando los componentes en cada eje:
fviz_contrib(pca, choice = "var", axes = 1, top = 10)
fviz_contrib(pca, choice = "var", axes = 2, top = 10)
fviz_contrib(pca, choice = "var", axes = 3, top = 10)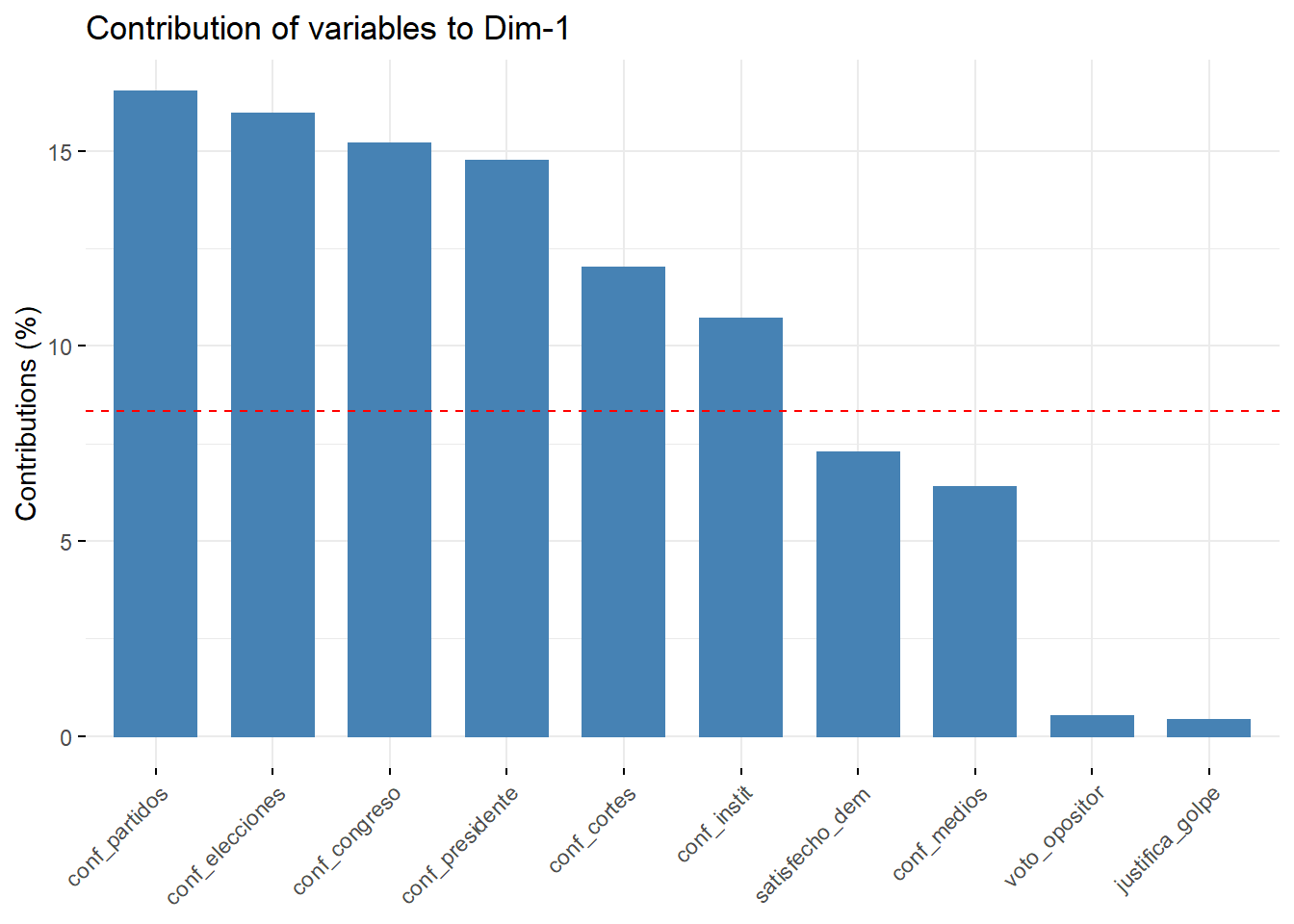
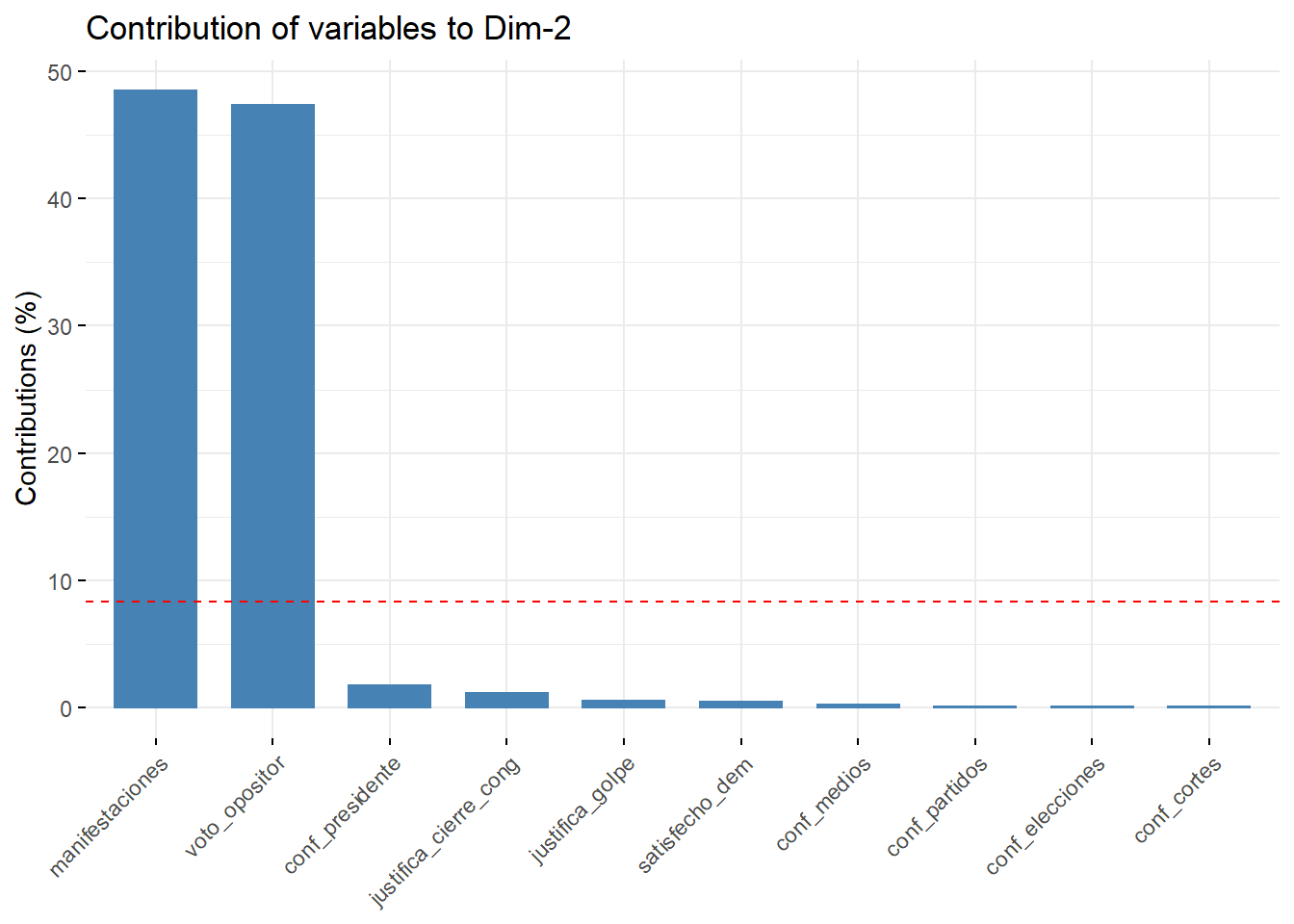
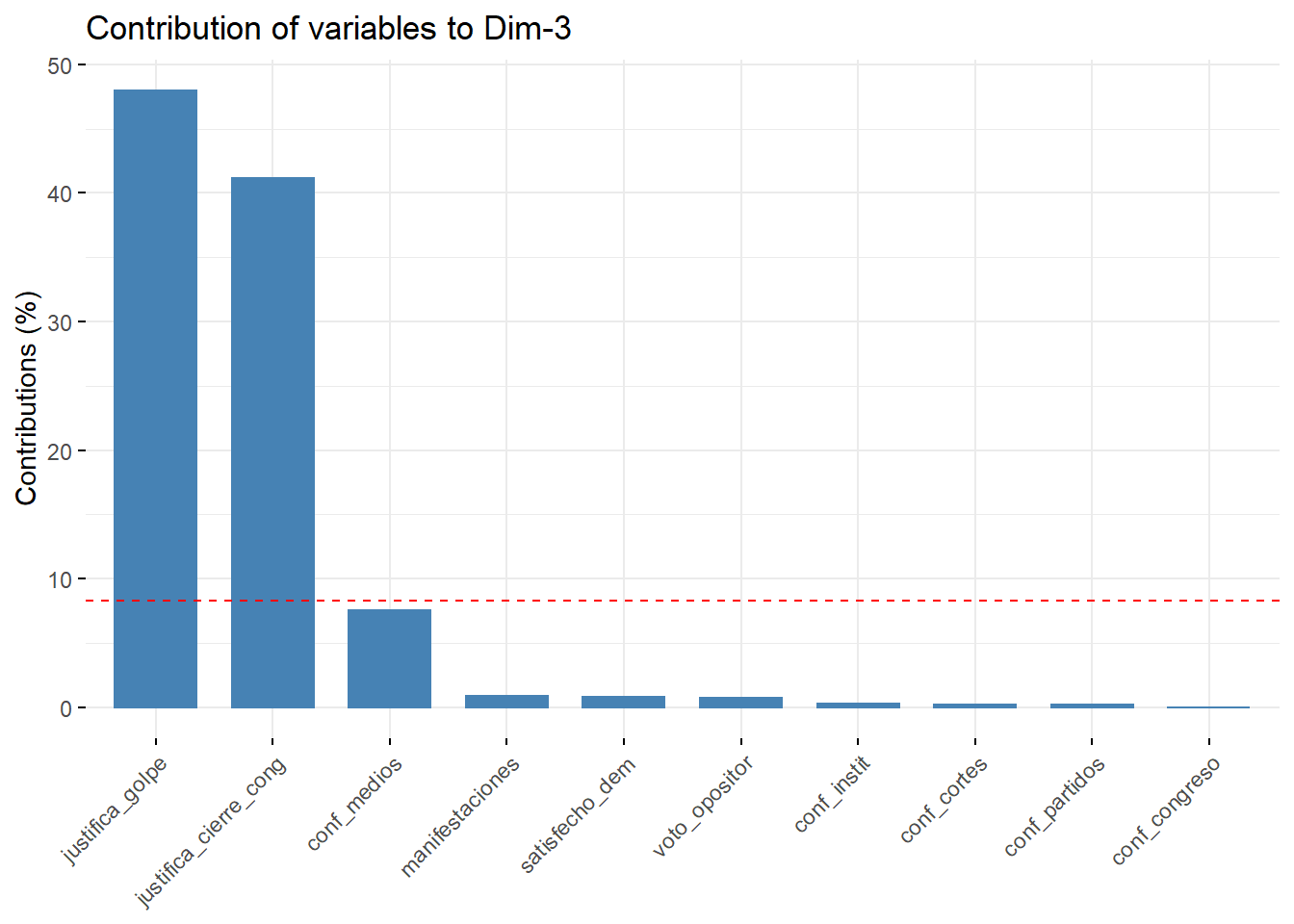
Figura 3.12: Las variables que contribuyen a cada dimensión en el PCA
Por ejemplo, el primer componente es el más diverso, pero se alimenta en gran medida de variables de confianza. Si recuerdas la matriz de correlación que hicimos con GGally, todas estas variables tenían altas correlaciones entre sí. El segundo componente se alimenta de la fuerte correlación entre manifestaciones y voto_opositor. La línea punteada roja expresa el valor que supondría un escenario en el que todas las variables contribuyen por igual, es decir, 1/12 (8,33%), y sirve sólo como referencia visual.
La composición de cada componente puede ayudarnos a nombrar cada dimensión del concepto que estamos creando. Esto nos dará más apoyo a la hora de justificar la forma en que se mide la opinión pública orientada hacia las instituciones políticas.
La primera dimensión, la que tiene mayor grado de variación, representa la confianza en instituciones como los poderes del Estado, los partidos políticos y las elecciones. Es la más diversa, pero se alimenta en gran medida de variables de confianza. Si recuerdas la matriz de correlación que hicimos con GGally, todas estas variables tenían altas correlaciones entre sí. Esto significa que cuando queremos medir la confianza en la política de los individuos, lo que nuestros datos representarán principalmente es esa confianza en la política más formal, en el concepto más clásico de la política.
La segunda de las dimensiones es la que denota el nivel de tolerancia política de la disidencia, que podría orientar una opinión hacia una forma de controlar los derechos de voto y de manifestación pública pacífica. Esto puede denotar lo propensos que están los ciudadanos a suspender ciertos derechos democráticos de aquellos que piensan de manera diferente.
La tercera dimensión, que representa el 10% de la varianza, es la compuesta por las variables que representan la propensión a justificar los golpes de Estado o los cierres del Congreso. Nuestro concepto tendrá entonces componentes que miden cómo se forman las opiniones individuales de las rupturas democráticas, midiendo cuán frágiles son las instituciones formales dentro de la opinión pública en América Latina.
Los resultados cualitativos de cada dimensión pueden ser representados en una tabla como esta:
| Dimensión | Etiqueta | Variables | Varianza explicada |
|---|---|---|---|
| 1 | Trust in institutions |
conf_cortes, conf_instit, conf_congreso, conf_presidente, conf_partidos, conf_elecciones
|
28.7% |
| 2 | Democratic rights |
voto_opositor, manifestaciones
|
12.3% |
| 3 | Anti-Democratic values |
justifica_golpe, justifica_cierre_cong
|
10.3% |
A medida que se crean estas nuevas dimensiones, pueden considerarse como nuevas variables a integrar en nuestra base de datos original, como se muestra a continuación:
lapop <- bind_cols(lapop, as_tibble(pca$scores))Éstas pueden tratarse como nuevas variables que pueden integrarse por separado en el análisis o, como veremos más adelante, integrarse en un índice de confianza en las instituciones políticas, que evalúa las tres dimensiones en su conjunto.
Ejercicio 15B. Estandariza y omite las NAs de las preguntas que elegiste en la primera parte para el sentimiento antiamericano. Realiza un Análisis de Componentes Principales y responde las siguientes preguntas: ¿Cuáles son los componentes más importantes? ¿Qué variables los componen? ¿Qué dimensiones están involucradas en el concepto de antiamericanismo que estás realizando?
15.5 Variación del concepto
Otra aplicación de esta herramienta en R permitirá generar un índice que caracterice a cada uno de los individuos diferenciando quiénes tienen más probabilidades de confiar en las instituciones y quiénes no. A partir de este índice individual, podremos entonces hacer una amplia variedad de estudios, desde comparaciones entre países, hasta comparaciones utilizando la edad, el género, los ingresos u otra variable de interés.
Para esta parte, generaremos de nuevo un PCA, pero esta vez lo haremos con el comando PCA del paquete FactoMineR. Esto nos dará el mismo resultado que el paquete anterior, pero queremos mostrar que esta herramienta puede ser utilizada de varias maneras en R.
library(FactoMineR)
pca_1 <- PCA(lapop_num, graph = F)Como vimos antes, debemos retener los componentes que contienen un Eigenvalor mayor que 1, que podemos ver de nuevo en el gráfico:
fviz_eig(pca_1, choice = "eigenvalue", addlabels = T, ylim = c(0, 3))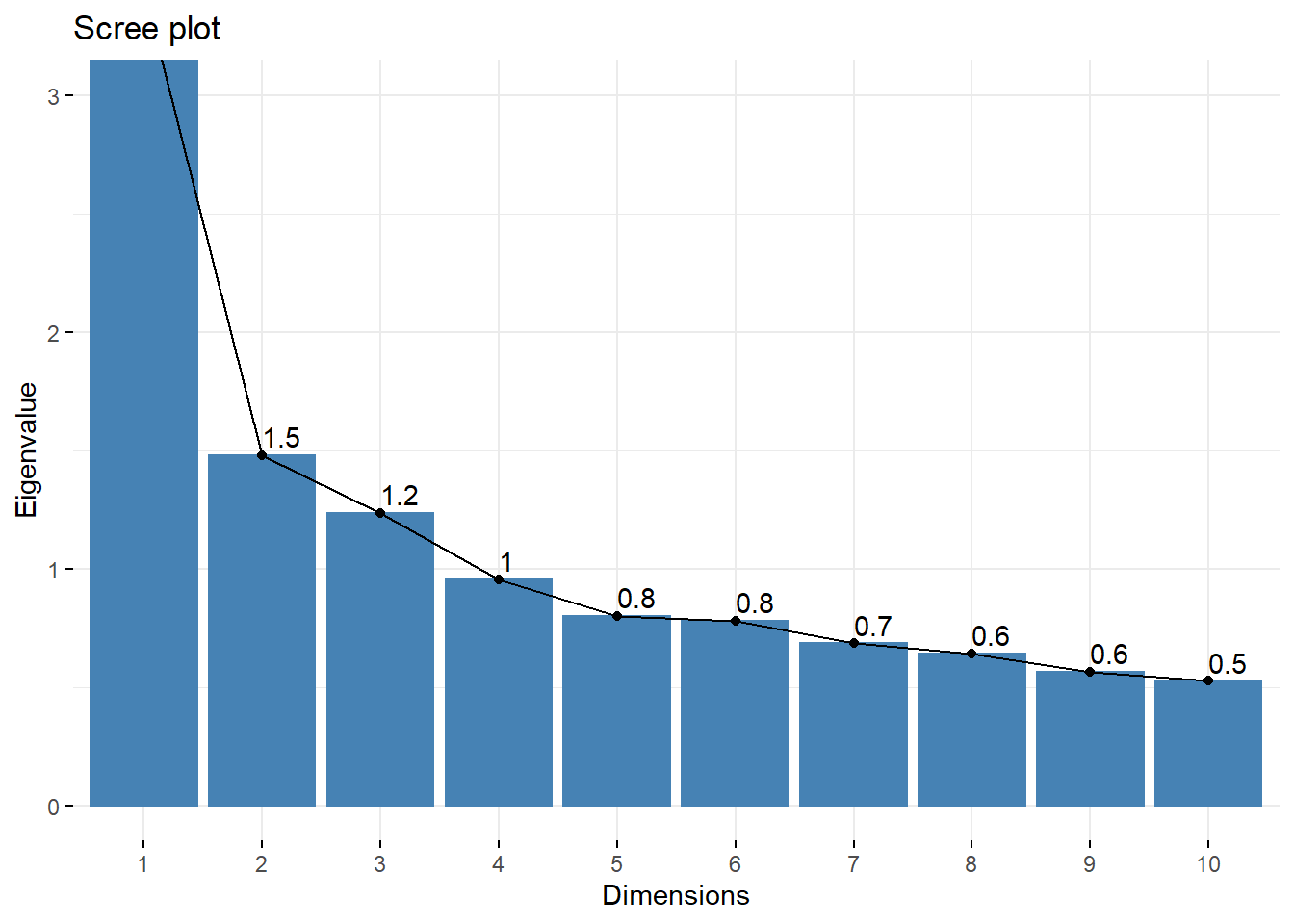
Figura 3.16: Eigenvalores de los componentes. Como regla general, retenemos los componentes con valores mayores que 1
Como pudimos ver de antemano, los componentes mayores de 1 son los tres primeros. Dejaremos en este caso el componente 4 para añadir más variables a nuestro índice. Hay un enorme grado de discrecionalidad en todo este proceso. Para condensar los componentes elegidos en una sola variable, es necesario recordar cuánta varianza acumulada representan del total:
eig <- get_eig(pca_1)
eig
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 3.44 28.7 29
## Dim.2 1.48 12.3 41
## Dim.3 1.23 10.3 51
## Dim.4 0.95 7.9 59
## Dim.5 0.80 6.6 66
## Dim.6 0.78 6.5 72
## [ reached getOption("max.print") -- omitted 6 rows ]Habíamos visto que los cuatro componentes representaban casi el 60% de la variación total: el primer componente 28,7%, el segundo 12,3%, el tercero 10,3% y el cuarto 7,9%. El siguiente paso es sumar estos cuatro componentes, pero ponderando cada uno de ellos por el porcentaje de la varianza que representan. Lo hacemos de la siguiente manera:
data_pca <- pca_1$ind$coord%>%
as_tibble() %>%
mutate(pca_01 = (Dim.1 * 28.7 + Dim.2 * 12.3 + Dim.3 * 10.3 +
Dim.4 * 7.9) / 60)
lapop <- bind_cols(lapop, data_pca %>% select(pca_01))Por lo tanto, hemos creado una única variable, que llamamospca_01. ¡Estamos muy cerca de tener esta variable como nuestro indicador de calificación de la democracia! Sucede que la variable pca_01 está en una escala poco amistosa. Idealmente queremos que nuestro indicador vaya de 0 a 1, de 0 a 10, o de 0 a 100 para que sea más fácil de interpretar. Haremos esto para que sea de 0 a 100, si quieres que sea de 0 a 10 o de 0 a 1 tienes que reemplazar 100 en la fórmula de abajo con el número que te interesa.
lapop <- lapop %>%
mutate(democracy_index = GGally::rescale01(pca_01) * 100)%>%
select(democracy_index, everything())Ya con nuestro nuevo índice reescalado, podemos ver cómo se ve su densidad:
index_density <- ggplot(data = lapop,
mapping = aes(x = democracy_index)) +
labs(x=" Índice de confianza en la democracia", y = "densidad") +
geom_density()
index_density 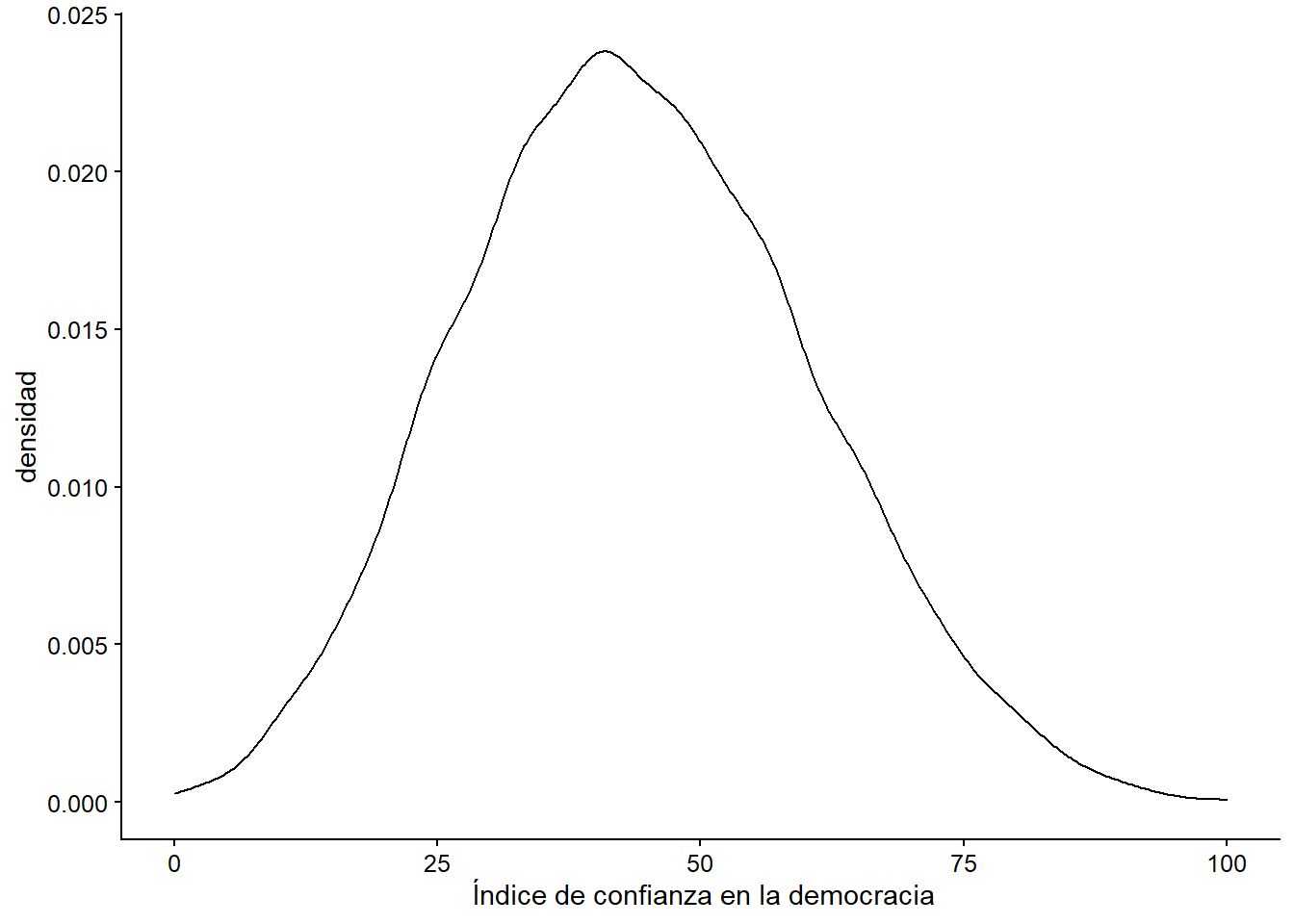
Figura 3.19: Gráfica de densidad de nuestro índice
Ahora que tenemos el índice listo, podemos hacer todo tipo de análisis. Por ejemplo, podemos hacer comparaciones por país. Si tuviéramos variables individuales, podríamos proceder a modelos de regresión con controles para el género, la ideología, los ingresos, el nivel de educación. Para hacer esto, puedes usar lo que aprendiste en los capítulos 7 y 8.
Descriptivamente, podemos hacer una comparación de cómo nuestro índice de confianza en las instituciones de los países de América Latina:
lapop <- lapop %>%
group_by(pais_nombre) %>%
mutate(democracy_avg = mean(democracy_index)) %>%
ungroup()
ggplot(lapop, aes(x = democracy_index)) +
geom_density() +
labs(title = " Confianza en la democracia en América Latina (N = 7000)",
x = " En azul el promedio de cada país",
y = "densidad") +
facet_wrap(~pais_nombre) +
geom_vline(aes(xintercept = democracy_avg),
color = "blue", linetype = "dashed", size = 1)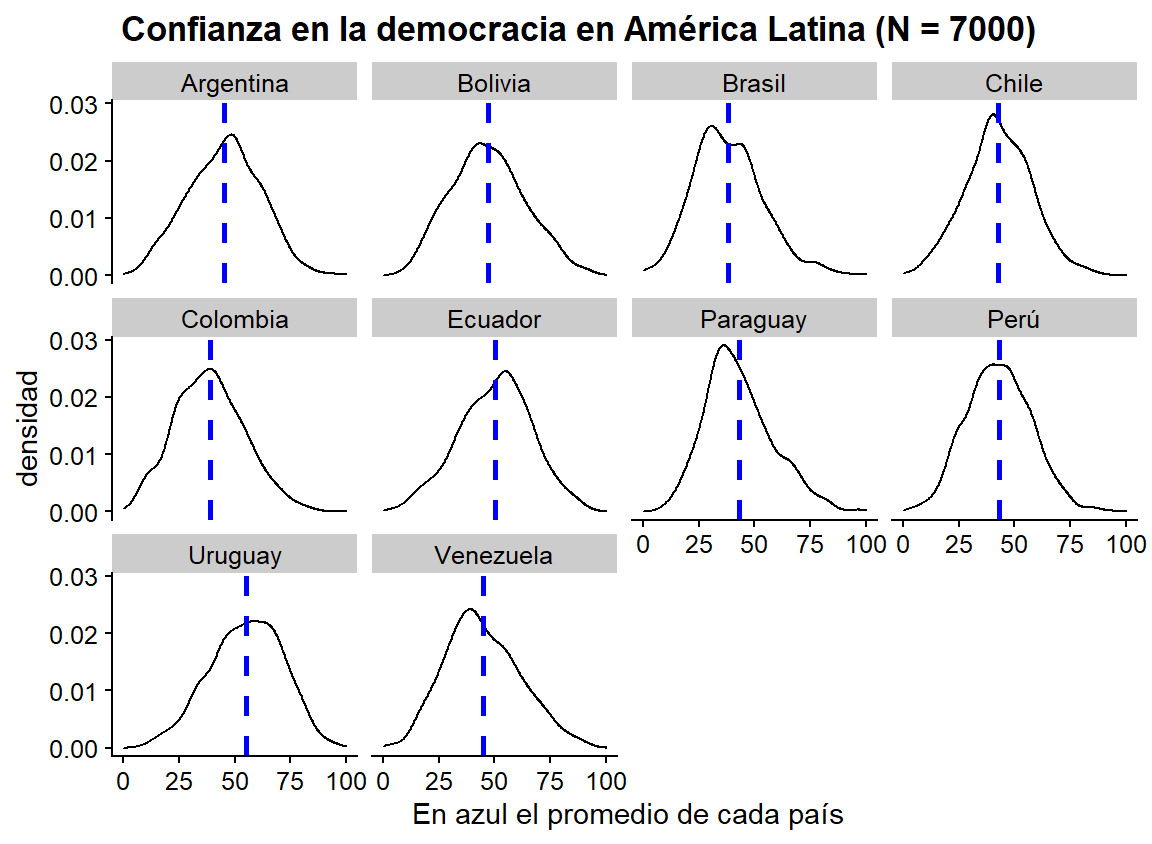
Figura 3.20: Gráficos de densidad de nuestro índice de confianza en la democracia por país. En azul, la media nacional
Ejercicio 15C. Utilizando el índice de confianza en la democracia en América Latina que acabamos de crear, analiza con modelos de regresión lineal qué variables tienen un alto poder explicativo sobre esta variable, son las variables de ideología, ingresos o edad importantes?
Ejercicio 15D. Con el conjunto de variables que elijas, crea un índice de antiamericanismo siguiendo las indicaciones del capítulo.
E-mail: cilabrin@uc.cl↩︎
E-mail: furdinez@uc.cl↩︎